
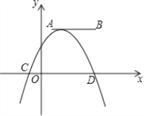
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为______.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:初中数学 来源: 题型:
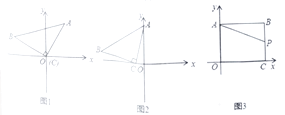
【题目】(1)操作思考:如图1,在平面直角坐标系中,等腰直角![]() 的直角顶点
的直角顶点![]() 在原点,将其绕着点
在原点,将其绕着点![]() 旋转,若顶点
旋转,若顶点![]() 恰好落在点
恰好落在点![]() 处.则①
处.则①![]() 的长为______;②点
的长为______;②点![]() 的坐标为______(直接写结果)
的坐标为______(直接写结果)
(2)感悟应用:如图2,在平面直角坐标系中,将等腰直角![]() 如图放置,直角顶点
如图放置,直角顶点![]() ,点
,点![]() ,试求直线
,试求直线![]() 的函数表达式.
的函数表达式.
(3)拓展研究:如图3,在直角坐标系中,点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,作
,作![]() 轴,垂足为点
轴,垂足为点![]() 是线段
是线段![]() 上的一个动点,点
上的一个动点,点![]() 是直线
是直线![]() 上一动点.问是否存在以点
上一动点.问是否存在以点![]() 为直角顶点的等腰直角
为直角顶点的等腰直角![]() ,若存在,请直接写出此时
,若存在,请直接写出此时![]() 点的坐标,若不存在,请说明理由.
点的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
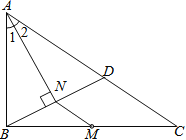
(1)求证:BN=DN;
(2)求△ABC的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题“计算:(2m4-4m3n-2m2n2)-(m4-2m2n2)+(-m4+4m3n-n3)的值,其中![]() ,n=-1.”小强不小心把
,n=-1.”小强不小心把![]() 错抄成了
错抄成了![]() ,但他的计算结果却也是正确的,你能说出这是为什么吗?
,但他的计算结果却也是正确的,你能说出这是为什么吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭![]() 出发,晚上停留在
出发,晚上停留在![]() 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
+5,-8,+10,-12,+6,-18,+5,-2.
(1)![]() 处在岗亭
处在岗亭![]() 的什么方向?距离岗亭
的什么方向?距离岗亭![]() 多远?
多远?
(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
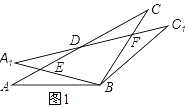
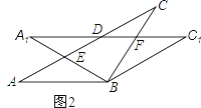
【题目】在△ABC中,AB=BC=2,∠ABC=120°,将△ABC绕点B顺时针旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
(1)如图1,观察并猜想,在旋转过程中,线段BE与BF有怎样的数量关系?并证明你的结论;
(2)如图2,当α=30°时,试判断四边形BC1DA的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数轴上有A,B两点,且AB=8,点A表示的数为6;动点P从点O出发,以每秒2个单位长度的速度沿数轴正方向运动,点Q从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
![]()
(1)写出数轴上点B表示的数是 ;
(2)当t=2时,线段PQ的长是 ;
(3)当0<t<3时,则线段AP= ;(用含t的式子表示)
(4)当PQ=![]() AB时,求t的值.
AB时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两城相距1000千米,一辆客车从甲城开往乙城,车速为![]() 千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为
千米/小时,同时一辆出租车从乙城开往甲城,车速为90千米/小时,设客车行驶时间为![]() (小时)
(小时)
(1)当![]() 时,客车与乙城的距离为 千米(用含
时,客车与乙城的距离为 千米(用含![]() 的代数式表示)
的代数式表示)
(2)已知![]() ,丙城在甲、乙两城之间,且与甲城相距260千米
,丙城在甲、乙两城之间,且与甲城相距260千米
①求客车与出租车相距100千米时客车的行驶时间;(列方程解答)
②已知客车与出租车在甲、乙之间的服务站![]() 处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
处相遇时,出租车乘客小王突然接到开会通知,需要立即返回,此时小王有两种返回乙城的方案:
方案一:继续乘坐出租车到丙城,加油后立刻返回乙城,出租车加油时间忽略不计;
方案二:在![]() 处换成客车返回乙城.
处换成客车返回乙城.
是通过计算,分析小王选择哪种方案能更快到达乙城?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某驻村扶贫小组为解决当地贫困问题,带领大家致富.经过调查研究,他们决定利用当地生产的甲乙两种原料开发A,B两种商品,为科学决策,他们试生产A、B两种商品100千克进行深入研究,已知现有甲种原料293千克,乙种原料314千克,生产1千克A商品,1千克B商品所需要的甲、乙两种原料及生产成本如下表所示.
甲种原料(单位:千克) | 乙种原料(单位:千克) | 生产成本(单位:元) | |
A商品 | 3 | 2 | 120 |
B商品 | 2.5 | 3.5 | 200 |
设生产A种商品x千克,生产A、B两种商品共100千克的总成本为y元,根据上述信息,解答下列问题:
(1)求y与x的函数解析式(也称关系式),并直接写出x的取值范围;
(2)x取何值时,总成本y最小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com