
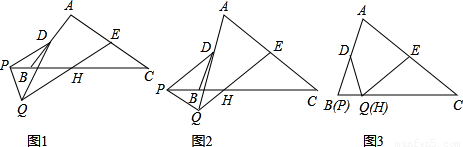
 ,即DF=kDE(DE=BF=
,即DF=kDE(DE=BF= BC),可证出△PDF∽△QDE.就有∠DFB=∠DEQ,又DE,BC平行可得∠DEQ=∠EHC,那么等量代换就有∠EHC=∠DFB=∠C,因此得证.
BC),可证出△PDF∽△QDE.就有∠DFB=∠DEQ,又DE,BC平行可得∠DEQ=∠EHC,那么等量代换就有∠EHC=∠DFB=∠C,因此得证. AC.
AC. AC.(1分)
AC.(1分) 证明:取BC边中点F,连接DE、DF.(2分)
证明:取BC边中点F,连接DE、DF.(2分) BC,
BC, AC,(4分)
AC,(4分) AC∴四边形DFCE是平行四边形.
AC∴四边形DFCE是平行四边形. .(7分)
.(7分) AC.(12分)
AC.(12分) AC.(1分)
AC.(1分) BC,DF∥AC且DF=
BC,DF∥AC且DF= AC,(4分)
AC,(4分) AC,∴四边形DFCE是平行四边形.
AC,∴四边形DFCE是平行四边形. AC.(10分)
AC.(10分) 选图3.结论:EH=
选图3.结论:EH= AC.(1分)
AC.(1分)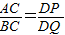 =k,
=k, AC.(6分)
AC.(6分)

科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(09)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2009年全国中考数学试题汇编《二次函数》(04)(解析版) 题型:解答题
 )在抛物线上,求m的值.
)在抛物线上,求m的值.
查看答案和解析>>
科目:初中数学 来源:2009年辽宁省大连市中考数学试卷(解析版) 题型:解答题
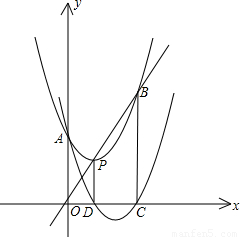
查看答案和解析>>
科目:初中数学 来源:2009年辽宁省大连市中考数学试卷(解析版) 题型:解答题
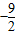 )在抛物线上,求m的值.
)在抛物线上,求m的值.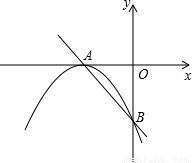
查看答案和解析>>
科目:初中数学 来源:2010年北京市中考模拟试卷汇总:圆(解析版) 题型:解答题
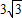 ,求BC的长.
,求BC的长.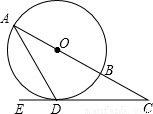
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com