

分析 (1)①由平行线的性质可得出∠PAB+∠PCD=180°,进而可得出∠AEC的度数;
②在图1中,过E作EF∥AB,根据平行线的性质可得出∠AEF=∠EAB、∠CEF=∠ECD,进而即可证出∠AEC=∠AEF+∠CEF=∠EAB+∠ECD;
(2)猜想:∠AEC=$\frac{1}{2}$∠APC,由角平分线的定义可得出∠EAB=$\frac{1}{2}$∠PAB、∠ECD=$\frac{1}{2}$∠PCD,由(1)可知∠AEC=∠EAB+∠ECD、∠APC=∠PAB+∠PCD,进而即可得出∠AEC=$\frac{1}{2}$(∠PAB+∠PCD)=$\frac{1}{2}$∠APC;
(3)在图3中,(2)中的结论不成立,而是满足∠AEC=180°-$\frac{1}{2}$∠APC,过P作PQ∥AB,由平行线的性质可得出∠PAB+∠APQ=180°、∠CPQ+∠PCD=180°,进而可得出∠PAB+∠PCD=360°-∠APC,再由角平分线的定义可得出∠EAB=$\frac{1}{2}$∠PAB、∠ECD=$\frac{1}{2}$∠PCD,结合(1)的结论即可证出∠AEC=180°-$\frac{1}{2}$∠APC.
解答 解:(1)①∵AB∥CD,
∴∠PAB+∠PCD=180°,
∴∠AEC=90°;
②证明:在图1中,过E作EF∥AB,则∠AEF=∠EAB.
∵AB∥CD,
∴EF∥CD,
∴∠CEF=∠ECD.
∴∠AEC=∠AEF+∠CEF=∠EAB+∠ECD.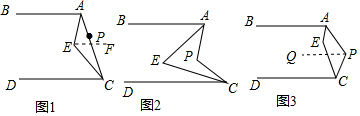
(2)猜想:∠AEC=$\frac{1}{2}$∠APC,理由如下:
∵AE、CE分别平分∠PAB和∠PCD,
∴∠EAB=$\frac{1}{2}$∠PAB,∠ECD=$\frac{1}{2}$∠PCD.
由(1)知∠AEC=∠EAB+∠ECD,∠APC=∠PAB+∠PCD,
∴∠AEC=$\frac{1}{2}$∠PAB+$\frac{1}{2}$∠PCD=$\frac{1}{2}$(∠PAB+∠PCD)=$\frac{1}{2}$∠APC.
(3)在图3中,(2)中的结论不成立,而是满足∠AEC=180°-$\frac{1}{2}$∠APC,
其证明过程是:
过P作PQ∥AB,则∠PAB+∠APQ=180°.
∵AB∥CD,
∴PQ∥CD,
∴∠CPQ+∠PCD=180°.
∴∠PAB+∠APQ+∠CPQ+∠PCD=360°,即∠PAB+∠PCD=360°-∠APC.
∵AE、CE分别平分∠PAB和∠PCD,
∴∠EAB=$\frac{1}{2}$∠PAB,∠ECD=$\frac{1}{2}$∠PCD.
由(1)知∠AEC=∠EAB+∠ECD,
∴∠AEC=$\frac{1}{2}$∠PAB+$\frac{1}{2}$∠PCD=$\frac{1}{2}$(∠PAB+∠PCD)=$\frac{1}{2}$(360°-∠APC)=180°-$\frac{1}{2}$∠APC.
点评 本题考查了平行线的判定与性质以及角平分线的定义,解题的关键是:(1)①根据平行线的性质找出∠PAB+∠PCD=180°;②根据“两直线平行,内错角相等”找出∠AEF=∠EAB、∠CEF=∠ECD;(2)根据角平分线的定义结合(1)结论找出∠AEC=$\frac{1}{2}$∠APC;(3)根据角平分线的定义结合(1)结论找出∠AEC=180°-$\frac{1}{2}$∠APC.


科目:初中数学 来源: 题型:选择题
| A. | x3+2x | B. | a2+b2 | C. | ${y}^{2}+y+\frac{1}{4}$ | D. | m2-4n2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{2}$ | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+2)(x-3) | B. | (x+6)(x-1) | C. | (x-2)(x+3) | D. | (x-6)(x+1) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
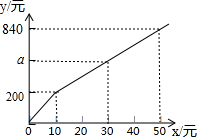 随着“中国诗词大会”节目的热播,《唐诗宋词精选》一书也随之热销.如果一次性购买10本以上,超过10本的那部分书的价格将打折,并依此得到付款金额y(单位:元)与一次性购买该书的数量x(单位:本)之间的函数关系如图所示,则下列结论错误的是( )
随着“中国诗词大会”节目的热播,《唐诗宋词精选》一书也随之热销.如果一次性购买10本以上,超过10本的那部分书的价格将打折,并依此得到付款金额y(单位:元)与一次性购买该书的数量x(单位:本)之间的函数关系如图所示,则下列结论错误的是( )| A. | 一次性购买数量不超过10本时,销售价格为20元/本 | |
| B. | a=520 | |
| C. | 一次性购买10本以上时,超过10本的那部分书的价格打八折 | |
| D. | 一次性购买20本比分两次购买且每次购买10本少花80元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com