
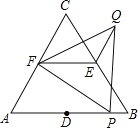
【题目】如图,△ABC和△FPQ均是等边三角形,点D、E、F分别是△ABC三边的中点,点P在AB边上,连接EF、QE.若AB=6,PB=1,则QE= .
【答案】2.
【解析】
试题分析:连结FD,根据等边三角形的性质,由△ABC为等边三角形得到AC=AB=6,∠A=60°,再根据点D、E、F分别是等边△ABC三边的中点,则AD=BD=AF=3,DP=2,EF为△ABC的中位线,于是可判断△ADF为等边三角形,得到∠FDA=60°,利用三角形中位线的性质得EF∥AB,EF=![]() AB=3,根据平行线性质得∠1+∠3=60°;又由于△PQF为等边三角形,则∠2+∠3=60°,FP=FQ,所以∠1=∠2,然后根据“SAS”判断△FDP≌△FEQ,所以DP=QE=2.
AB=3,根据平行线性质得∠1+∠3=60°;又由于△PQF为等边三角形,则∠2+∠3=60°,FP=FQ,所以∠1=∠2,然后根据“SAS”判断△FDP≌△FEQ,所以DP=QE=2.
解:连结FD,如,
∵△ABC为等边三角形,
∴AC=AB=6,∠A=60°,
∵点D、E、F分别是等边△ABC三边的中点,AB=6,PB=1,
∴AD=BD=AF=3,DP=DB﹣PB=3﹣1=2,EF为△ABC的中位线,
∴EF∥AB,EF=![]() AB=3,△ADF为等边三角形,
AB=3,△ADF为等边三角形,
∴∠FDA=60°,
∴∠1+∠3=60°,
∵△PQF为等边三角形,
∴∠2+∠3=60°,FP=FQ,
∴∠1=∠2,
∵在△FDP和△FEQ中
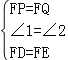 ,
,
∴△FDP≌△FEQ(SAS),
∴DP=QE,
∵DP=2,
∴QE=2.
故答案为:2.


 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】(1)4﹣(﹣2)﹣2﹣32÷(3.14﹣π)0
(2)(3![]() )12×(
)12×(![]() )11×(一2)3
)11×(一2)3
(3)5a(a2﹣3a+1)﹣a2(1﹣a)
(4)(﹣a)3(﹣2ab2)3﹣4ab2(a5b4﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(0,α),B(b,α),且α、b满足(a﹣2)2+|b﹣4|=0,现同时将点A,B分别向下平移2个单位,再向左平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,AB.
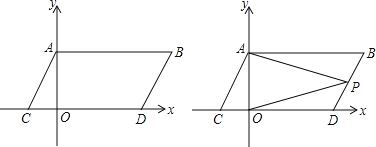
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABCD
(2)在y轴上是否存在一点M,连接MC,MD,使S△MCD=S四边形ABDC?若存在这样一点,求出点M的坐标,若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PA,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,并说明理由.
的值是否发生变化,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() (k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=
(k>0)交于A、B两点,点B的坐标为(﹣4,﹣2),C为双曲线y=![]() (k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .
(k>0)上一点,且在第一象限内,若△AOC的面积为6,则点C的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在Rt△ABC中,∠C=90°,点D是线段CA延长线上一点,且AD=AB.点F是线段AB上一点,连接DF,以DF为斜边作等腰Rt△DFE,连接EA,EA满足条件EA⊥AB.

(1)若∠AEF=20°,∠ADE=50°,AC=2,求AB的长度;
(2)求证:AE=AF+BC;
(3)如图2,点F是线段BA延长线上一点,探究AE、AF、BC之间的数量关系,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com