
【题目】为了解某市九年级学生学业考试体育成绩,现随机抽取部分学生的体育(A:50分;B:49﹣45分;C:44﹣40分;D:39﹣30分;E:29﹣0分)成绩进行分段统计如下:

根据上面提供的信息,回答下列问题:
(1)在统计表中,a的值为 ,b的值为 ;
(2)将统计图补充完整;
(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10560名九年级学生中体育成绩为优秀的学生人数约有多少名?
 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】小明所在城市的“阶梯水价”收费办法是:每户用水不超过5吨,每吨水费x元;超过5吨,超过部分每吨加收2元,小明家今年5月份用水9吨,共交水费为44元,根据题意列出关于x的方程正确的是( )
A. 5x+4(x+2)=44 B. 5x+4(x﹣2)=44 C. 9(x+2)=44 D. 9(x+2)﹣4×2=44
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°,AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:
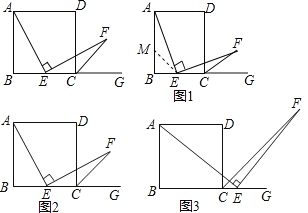
(1)经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
问题:如图所示,在正方形ABCD和BEFG中,点A,B,E在同一直线上,P是线段DF中点,连接PG,PC.
探究:当PG与PC的夹角为90°时,平行四边形BEFG是正方形.
小聪同学的思路是:首先可以证明四边形BEFG是矩形,然后延长GP交DC于点H,构造全等三角形,经过推理可以探索出问题答案.
请你参考小聪同学的思路,探究并解决这个问题.
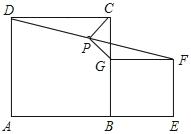
(1)求证:四边形BEFG是矩形;
(2)求证:PG与PC的夹角为90°时,四边形BEFG是正方形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com