
问题:你能很快算出![]() 吗?
吗?
为了解决这个问题,我们考察个位上的数字为5的自然数的平方。任意一个个位数为5的自然数可写成10n+5,即求![]() 的值(n为自然数)。你分析n=1,n=2,n=3…这些简单情况,从中探索其规律,并归纳、猜想出结论(在下面空格内填上你的探索结果)。
的值(n为自然数)。你分析n=1,n=2,n=3…这些简单情况,从中探索其规律,并归纳、猜想出结论(在下面空格内填上你的探索结果)。
(1)通过计算,探索规律:
![]() =225可写成100×1×(1+1)+25,
=225可写成100×1×(1+1)+25,
![]() =625可写成100×2×(2+1)+25,
=625可写成100×2×(2+1)+25,
![]() =1225可写成100×3×(3+1)+25,
=1225可写成100×3×(3+1)+25,
![]() =2025可写成100×4×(4+1)+25,
=2025可写成100×4×(4+1)+25,
……
![]() =5625可写成________,
=5625可写成________,
![]() =7225可写成________,
=7225可写成________,
……
(2)从第(1)题的结果,归纳、猜想得:
![]() =________.
=________.
(3)根据上面的归纳、猜想,请计算:
![]() =________.
=________.
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:数学教研室 题型:044
你能很快算出 吗?
吗?
为了解决这个问题,我们考查个位上的数为5的自然数的平方,任意一个个位数字为5的自然数都可以写成10n+5,即求 的值,(n为自然数),你试分析n=1,n=2,n=3…,这些情况探索其规律,猜想结论.
的值,(n为自然数),你试分析n=1,n=2,n=3…,这些情况探索其规律,猜想结论.
(1)通过计算,探索规律:
 ,
,
 ,
,
 ,
,
…
 =______,
=______,
…
(2)由第(1)题的结果,归纳猜想得 =______;
=______;
(3)根据上面的归纳猜想计算 =______.
=______.
查看答案和解析>>
科目:初中数学 来源: 题型:044
你能很快算出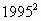 吗?为了解决这个问题,我们考察个位上的数为5的自然数的平方,任意一个个位数为5的自然数都可以写成10·n+5,即求
吗?为了解决这个问题,我们考察个位上的数为5的自然数的平方,任意一个个位数为5的自然数都可以写成10·n+5,即求 的值(n为自然数).你试分析n=1,n=2,n=3,…这递增简单情况,从中探索其规律,并归纳、推测出结论(在下面空格内填上你的探索结果).
的值(n为自然数).你试分析n=1,n=2,n=3,…这递增简单情况,从中探索其规律,并归纳、推测出结论(在下面空格内填上你的探索结果).
(1)通过计算,探索规律:
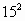 =225可写成100×1(1+1)+25,
=225可写成100×1(1+1)+25,
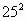 =625可写成100×2(2+1)+25,
=625可写成100×2(2+1)+25,
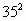 =1225可写成100×3(3+1)+25,
=1225可写成100×3(3+1)+25,
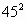 =2025可写成100×4(4+1)+25,
=2025可写成100×4(4+1)+25,
…
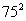 =5625可写成________,
=5625可写成________,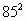 =7225可写成________;
=7225可写成________;
(2)从第(1)题的结果,归纳、推测得: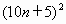 =________;
=________;
(3)根据上面的归纳、推测,请算出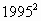 =________.
=________.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com