
【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图方式叠放在一起(其中,∠A=60°,∠D=30°;∠E=∠B=45°):
(1)①若∠DCE=35°,求∠ACB的度数;
②若∠ACB=150°,求∠DCE的度数;
(2)由(1)猜想∠ACB与∠DCE的数量关系,并说明理由.
(3)请你动手操作,现将三角尺ACD固定,三角尺BCE的CE边与CA边重合,绕点C顺时针方向旋转,当0°<∠ACE<180°且点E在直线AC的上方时,这两块三角尺是否存在一组边互相平行?若存在,请直接写出∠ACE角度所有可能的值(不必说明理由);若不存在,请说明理由.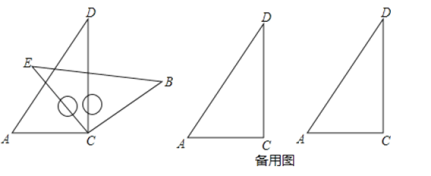
【答案】解:(1)①∵∠ECB=90°,∠DCE=35°,
∴∠DCB=90°﹣35°=55°,
∴∠ACB=∠ACD+∠DCB=90°+55°=145°;
②∵∠ACB=150°,∠ACD=90°,
∴∠DCB=150°﹣90°=60°,
∴∠DCE=90°﹣60°=30°;
(2)∠ACB+∠DCE=180°,
∵∠ACB=∠ACD+∠DCB=90°+∠DCB,
∴∠ACB+∠DCE=90°+∠DCB+∠DCE=90°+90°=180°;
(3)存在,
当∠ACE=30°时,AD∥BC,
当∠ACE=∠E=45°时,AC∥BE,
当∠ACE=120°时,AD∥CE,
当∠ACE=135°时,BE∥CD,
当∠ACE=165°时,BE∥AD.
【解析】(1)①先根据直角三角板的性质求出∠ACE及∠DCB的度数,进而可得出∠ACB的度数;
②由∠ACB=150°,∠ACD=90°,可得出∠DCB的度数,进而得出∠DCE的度数;
(2)根据①中的结论可提出猜想,再由∠ACB=∠ACD+∠DCB,∠ACB+∠DCE=90°+∠DCB+∠DCE可得出结论;
(3)分∠ACE=30°,45°,120°,135°及165°进行解答.
【考点精析】本题主要考查了平行线的判定和三角形的内角和外角的相关知识点,需要掌握同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC平分∠BAD,CE⊥AB于点E,∠ADC+∠ABC=180°,有下列结论:①CD=CB;②AD+AB=2AE;③∠ACD=∠BCE;④AB-AD=2BE.其中正确的是( )

A. ② B. ①②③ C. ①②④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在DF上,点B在AC上,∠1=∠2,∠C=∠D.
试说明:AC∥DF.将过程补充完整.
解:∵∠1=∠2( )
∠1=∠3( )
∴∠2=∠3()
∴∥ ( )
∴∠C=∠ABD ( )
又∵∠C=∠D()
∴∠D=∠ABD( )
∴AC∥DF( )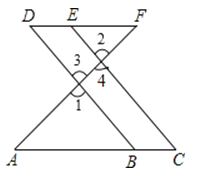
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.减去一个数等于加上这个数
B.两个相反数相减得0
C.两个数相减,差一定小于被减数
D.两个数相减,差不一定小于被减数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF=( )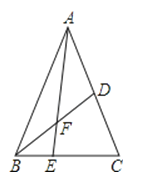
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中不能使两个直角三角形全等的是( )
A. 两条直角边对应相等 B. 两个锐角对应相等
C. 一条直角边和斜边对应相等 D. 一个锐角和斜边对应相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com