
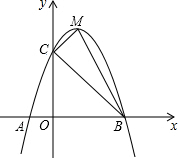
 如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.
如图,抛物线y=ax2+bx+c交x轴于A(-1,0)、B两点,交y轴于点C(0,5),且过点D(1,8),M为其顶点.分析 (1)由A、C、D三点在抛物线上,根据待定系数法即可求出抛物线的解析式;
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=$\frac{1}{2}$MN•OB;
(3)先由△PAB的面积等于△MCB的面积,求出AB边上的高即点P的纵坐标的绝对值,再将点P的纵坐标代入抛物线的解析式,得到一元二次方程,如果方程有实数根,则在抛物线上存在点P,否则不存在.
解答 解:(1)∵A(-1,0),C(0,5),D(1,8)三点在抛物线y=ax2+bx+c上,
∴$\left\{\begin{array}{l}{0=a-b+c}\\{5=c}\\{8=a+b+c}\end{array}\right.$,
解方程组,得$\left\{\begin{array}{l}{a=-1}\\{b=4}\\{c=5}\end{array}\right.$,
故抛物线的解析式为y=-x2+4x+5;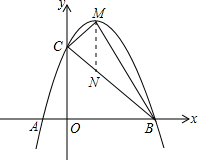 (2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=$\frac{1}{2}$MN•OB.
(2)过点M作MN∥y轴交BC轴于点N,则△MCB的面积=△MCN的面积+△MNB的面积=$\frac{1}{2}$MN•OB.
∵y=-x2+4x+5=-(x-5)(x+1)=-(x-2)2+9,
∴M(2,9),B(5,0),
由B、C两点的坐标易求得直线BC的解析式为:y=-x+5,
当x=2时,y=-2+5=3,则N(2,3),
则MN=9-3=6,
则S△MCB=$\frac{1}{2}$×6×5=15;
(3)在抛物线上存在点P,使△PAB的面积等于△MCB的面积.理由如下:
∵A(-1,0),B(5,0),
∴AB=6,
∵△PAB的面积=△MCB的面积,
∴$\frac{1}{2}$×6×|yP|=15,
∴|yP|=5,yP=±5.
当yP=5时,-x2+4x+5=5,解得x1=0,x2=4;
当yP=-5时,-x2+4x+5=-5,解得x3=2+$\sqrt{14}$,x4=2-$\sqrt{14}$.
故在抛物线上存在点P1(0,5),P2(4,5),P3(2+$\sqrt{14}$,-5),P3(2-$\sqrt{14}$,-5),使△PAB的面积等于△MCB的面积.
点评 本题考查了待定系数法求二次函数的解析式,确定特殊点的坐标,三角形的面积,正确的理解题意是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.
如图所示,已知OB、OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD,若∠AOD=96°,∠MON=68°,求∠BOC的大小.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 至少有1个球是白球 | B. | 至少有1个球是黑球 | ||
| C. | 至少有2个球是黑球 | D. | 至少有2个球是白球 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
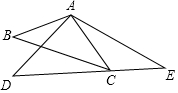 如图,△ABC和△ADE中,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,∠BAD=20°,则∠BCD=20度.
如图,△ABC和△ADE中,$\frac{AB}{AD}$=$\frac{BC}{DE}$=$\frac{AC}{AE}$,∠BAD=20°,则∠BCD=20度.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.78×107 | B. | 2.78×108 | C. | 2.78×106 | D. | 27.8×107 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
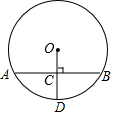 如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )
如图,已知半径OD与弦AB互相垂直,垂足为点C,若AB=8,CD=3,则⊙O的半径为( )| A. | $\frac{19}{6}$ | B. | 4 | C. | 5 | D. | $\frac{25}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
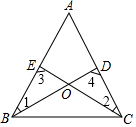 如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O,给出下列三个条件:①∠1=∠2;②∠3=∠4;③BE=CD.
如图,在△ABC中,D,E分别是AC,AB上的点,BD与CE交于点O,给出下列三个条件:①∠1=∠2;②∠3=∠4;③BE=CD.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com