
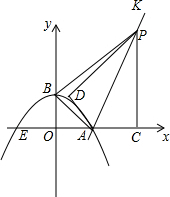
 ��֪����ͼ��������y=ax2+bx+2��x�ύ�ڵ�A��4��0����E��-2��0�����㣬����AB������A��ֱ��AK��AB������P��A�������ÿ��$\sqrt{5}$����λ���ȵ��ٶ�������AK�˶������˶�ʱ��Ϊt�룬����P��PC��x�ᣬ����ΪC���ѡ�ACP��AP���ۣ�ʹ��C���ڵ�D����
��֪����ͼ��������y=ax2+bx+2��x�ύ�ڵ�A��4��0����E��-2��0�����㣬����AB������A��ֱ��AK��AB������P��A�������ÿ��$\sqrt{5}$����λ���ȵ��ٶ�������AK�˶������˶�ʱ��Ϊt�룬����P��PC��x�ᣬ����ΪC���ѡ�ACP��AP���ۣ�ʹ��C���ڵ�D�������� ��1���ô���ϵ������������߽���ʽ��
��2���ȸ��ݵ�D�ڡ�APB�ڲ������t�ķ�Χ��Ȼ���á�APB��ȥ��APC���������ص��IJ��������
��3�����������ľ��빫ʽ��ʾ��BP�����������������̣����ʱ�䣻
��4�����жϳ���D����O�ľ�����Сʱ��λ�ã�Ȼ�������Ǻ������ɶ������㣮
��� �⣺��1����A��B��E������������߽���ʽ�У���
$\left\{\begin{array}{l}{16a+4b+c=0}\\{4a-2b+c=0}\\{c=2}\end{array}\right.$��
��$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=\frac{1}{2}}\\{c=2}\end{array}\right.$
��y=-$\frac{1}{4}$x2+$\frac{1}{2}$x+2��
��2����A��4��0����B��0��2��
��ֱ��AB����ʽΪy=-$\frac{1}{2}$x+2��
��AB��AK��
��ֱ��AK����ʽΪy=2x+8��
��tan��PAC=$\frac{PC}{AC}$=2��
��AP=$\sqrt{5}$t��
��AC=t��PC=2t��
��D�ڡ�ABP�ڲ���
���APB����APC��
��tan��APB��tan��APC��
��$\frac{AB}{AP}��\frac{AC}{PC}$��
��$\frac{2\sqrt{5}}{\sqrt{5}t}=\frac{t}{2t}$��
��t��4��
��0��t��4��
��S=S��APB-S��APD
=S��APB-S��APC
=$\frac{1}{2}$��AB��AP-$\frac{1}{2}$��AC��PC
=$\frac{1}{2}$��2$\sqrt{5}$��$\sqrt{5}$t-$\frac{1}{2}$��t��2t
=-t2+5t��0��t��4��
��3����P��t+4��2t����
��BP=$\sqrt{A{B}^{2}+A{P}^{2}}$=$\sqrt{20+5{t}^{2}}$��
���߶�AC�ij����߶�BP����$\frac{1}{3}$��
��t=$\frac{1}{3}$$\sqrt{20+5{t}^{2}}$��
��t=-$\sqrt{5}$���ᣩt=$\sqrt{5}$
��4��Ҫʹ��D��O�ľ�����С�����е�D��OP�ϣ���ʱ����D1
��Rt��OCP��tan��POC=$\frac{PC}{OC}$=$\frac{2t}{t+4}$��
��Rt��OCP��tan��AOC=$\frac{A{D}_{1}}{O{D}_{1}}=\frac{t}{O{D}_{1}}$��
��$\frac{2t}{t+4}=\frac{t}{O{D}_{1}}$��
��OD1=$\frac{t+4}{2}$��
���ݹ��ɶ����ã�OD12+AD12=OA2��
�ࣨ$\frac{t+4}{2}$��2+t2=16��
��t=-4���ᣩt=$\frac{12}{5}$��
��OD1=$\frac{t+4}{2}$=$\frac{16}{5}$��
�ද��D����O�ľ�����С����Ϊ$\frac{16}{5}$��
���� �����Ƕ��κ����ۺ��⣬��Ҫ�����˴���ϵ������������Ǻ��������ɶ���������ļ��㣬�Ȿ��Ĺؼ���ȷ����ʱ��ķ�Χ��


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a-2=-$\frac{1}{{a}^{2}}$��a��0�� | B�� | $\sqrt{��-2��^{2}}$=-2 | C�� | a0=0��a��0�� | D�� | $\root{3}{��-2��^{3}}$=-2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
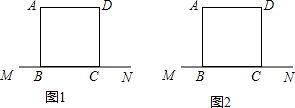 ��֪������ABCD��ͼ��ʾ��M��N��ֱ��BC�ϣ�MB=NC���Էֱ���ͼ1��ͼ2�н����̶ȵ�ֱ����һ����ͬ�ĵ���������OMN��
��֪������ABCD��ͼ��ʾ��M��N��ֱ��BC�ϣ�MB=NC���Էֱ���ͼ1��ͼ2�н����̶ȵ�ֱ����һ����ͬ�ĵ���������OMN���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��l1��ֱ��l2���ഹֱ��A��B���������㣮C��D�ֱ���ֱ��l1��l2�ϵĶ��㣮��ȷ��C��D�����λ�ã�ʹ�ı���ACDB���ܳ���̣�
��ͼ��ֱ��l1��ֱ��l2���ഹֱ��A��B���������㣮C��D�ֱ���ֱ��l1��l2�ϵĶ��㣮��ȷ��C��D�����λ�ã�ʹ�ı���ACDB���ܳ���̣��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a0=1 | B�� | $\sqrt{9}$=��3 | C�� | ��ab��2=ab2 | D�� | ��-a2��3=-a6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��x3��2=x5 | B�� | x3•x2=x5 | C�� | ��2x��2=2x2 | D�� | ��x+2��2=x2+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a8��a4=a2 | B�� | a3•a4=a12 | C�� | $\sqrt{4}$=��2 | D�� | 2x3•x2=2x5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
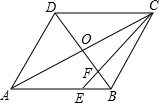 ��ͼ����?ABCD�У�AC��BD���ڵ�O��EΪAB��һ�㣬��AE=2EB������CE��BD�ڵ�F����S��BEF��S��COF�ı�ֵΪ��������
��ͼ����?ABCD�У�AC��BD���ڵ�O��EΪAB��һ�㣬��AE=2EB������CE��BD�ڵ�F����S��BEF��S��COF�ı�ֵΪ��������| A�� | 1��3 | B�� | 1��2 | C�� | 2��3 | D�� | 3��4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com