
【题目】因式分解:(1)﹣2![]() +12a﹣18a (2)(x+4)-16x
+12a﹣18a (2)(x+4)-16x
(3)(x-2x)+2(x-2x)+1 (4)-28![]() n+42m
n+42m![]() -14m n
-14m n
【答案】(1)-2a(a-3) ;(2) (x+2)(x-2);(3)![]() ;(4)﹣14mn(2mn﹣3n+1).
;(4)﹣14mn(2mn﹣3n+1).
【解析】
(1)原式提取a后,利用完全平方公式分解即可;(2)原式利用平方差公式分解,再利用完全平方公式分解即可;(3)原式利用完全平方公式分解即可;(4) 首先提取负号,注意括号里的各项都要改变符号,再找出多项式的公因式,然后提取公因式法因式分解即可.
(1)原式=-2a(a2-6a+9) =-2a(a-3)2 ;
(2)原式=(x2+4+4x)(x2+4-4x)=(x+2)2(x-2)2;
(3)原式=(x2-2x+1)2= (x-1)4
(4)原式=﹣(28m3n2﹣42m2n3+14m2n)=﹣14m2n(2mn﹣3n2+1).


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=2,BC=1.把△ABC分别绕直线AB和BC旋转一周,所得几何体的地面圆的周长分别记作l1 , l2 , 侧面积分别记作S1 , S2 , 则( )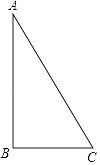
A.l1:l2=1:2,S1:S2=1:2
B.l1:l2=1:4,S1:S2=1:2
C.l1:l2=1:2,S1:S2=1:4
D.l1:l2=1:4,S1:S2=1:4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.
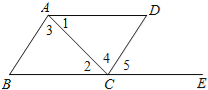
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,经过点A的⊙O与BC相切于点D,交AB于点E. 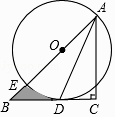
(1)求证:AD平分∠BAC;
(2)若CD=1,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
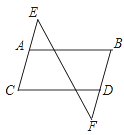
【题目】如图,有以下3句话:①AB∥CD,②∠B=∠C、③∠E=∠F、请以其中2句话为条件,第三句话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题?请加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
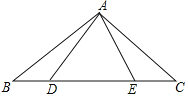
【题目】如图,点D,E在△ABC的边BC上,连接AD,AE.有下面三个等式:①AB=AC;②AD=AE;③BD=CE.以此三个等式中的两个作为命题的题设,另一个作为命题的结论,相构成三个命题.解答下列问题
(1)写出这三个命题,并直接判断其是否是真命题;
(2)请选择一个真命题进行证明(先写出所选命题,然后证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧 ![]() 于点P,Q,且点P,Q在AB异侧,连接OP.
于点P,Q,且点P,Q在AB异侧,连接OP. 
(1)求证:AP=BQ;
(2)当BQ=4 ![]() 时,求
时,求 ![]() 的长(结果保留π);
的长(结果保留π);
(3)若△APO的外心在扇形COD的内部,求OC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(3,1),B(8,5),若用(3,1)→(3,3)→(5,3)→(5,4)→(8,4)→(8,5)表示由A到B的一种走法,并规定从A到B只能向上或向右走,请用上述表示法写出另两种走法,并判断这几种走法的路程是否相等。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com