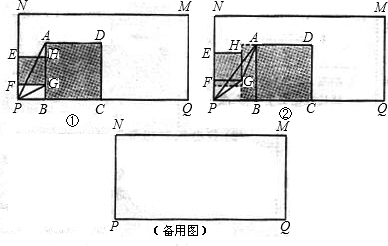
如图①，在长为6厘米，宽为3厘米的矩形PQMN中，有两张边长分别为二厘米和一厘米的正方形纸片ABCD和EFGH，且BC且在PQ上，PB=1厘米，PF=
厘米，从初始时刻开始，纸片ABCD沿PQ以2厘米每秒的速度向右平移，同时纸片EFGH沿PN以1厘米每秒的速度向上平移，当C点与Q点重合时，两张图片同时停止移动，设平移时间为t秒时，（如图②），纸片ABCD扫过的面积为S
1，纸片EFGH扫过的面积为S
2，AP，PG，GA所围成的图形面积为S（这里规定线段面积为零，扫过的面积含纸片面积）．解答下列问题：
（1）当t=
时，PG=
，PA=
时，PA
PG+GA（填=或≠）；
（2）求S与t之间的关系式；
（3）请探索是否存在t值（t＞
），使S
1+S
2=4S+5．若存在，求出t值；若不存在，说明理由．
七彩题卡口算应用一点通系列答案
