
【题目】如图,菱形ABCD中,AB=2,∠BAD=60°,E是AB的中点,P是对角线AC上的一个动点,则PE+PB的最小值是 . 
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
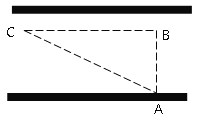
【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:

(1)这三个厂家的广告,分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?
(2)如果三个厂家产品的售价一样,作为顾客的你选购哪个厂家的产品?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC 的顶点分别为 A(-2,2)、B(-4,5)、C(-5,1)和直线 m (直线 m 上各点的 横坐标都为 1).
(1)作出△ABC 关于 x 轴对称的图形△A1B1C1,并写出点 B1 的坐标;
(2)作出△ABC 关于 y 轴对称的图形△A2 B2C2,并写出点 B2 的坐标;
(3)若点 P( a,b )是△ABC 内部一点,写出点 P 关于直线 m 对称的点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
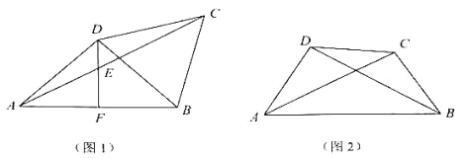
【题目】在四边形 ABCD 中,BC=CD,连接 AC、BD,∠ADB=90°.
(1)如图 1,若 AD=BD=BC,过点 D 作 DF⊥AB 于点 F,交 AC 于点 E:
①求∠DAC;
②猜想 AE、DE、CE 的数量关系,并证明你的猜想;
(2)如图 2,若 AC=BD,求∠DAC 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的 ![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】7张如图1的长为a,宽为b(a>b)的小长方形纸片,按图2的方式不重叠地放在矩形ABCD内,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a,b满足( )

A.a=![]() bB.a=3bC.a=
bB.a=3bC.a=![]() bD.a=4b
bD.a=4b
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com