
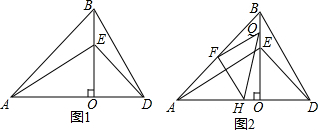
分析 (1)结论:AE=BD,AE⊥BD.如图1中,延长AE交BD于F.由△AOE≌△BOD,推出AE=BD,∠EAO=∠OBD,由∠AEO=∠BEF,推出∠BFE=∠AOE=90°,即∠BFE=90°;
(2)结论:FQ=FH,FQ⊥FH.根据三角形中位线定理即可即可解决问题.
(3)△FQH是等腰直角三角形,求出FQ即可解决问题.
解答 解:(1)结论:AE=BD,AE⊥BD.
理由:如图1中,延长AE交BD于F.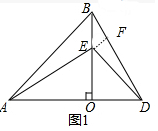
在△AOE和△BOD中,
$\left\{\begin{array}{l}{OA=OB}\\{∠AOE=∠BOD}\\{OE=OD}\end{array}\right.$,
∴△AOE≌△BOD,
∴AE=BD,∴∠EAO=∠OBD,
∵∠AEO=∠BEF,
∴∠BFE=∠AOE=90°,
∴∠BFE=90°,
∴AE⊥BD,AE=BD.
(2)结论:FQ=FH,FQ⊥FH.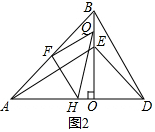
理由:∵BF=AF,BQ=QE,
∴FQ∥AE.FQ=$\frac{1}{2}$AE,
∵AF=FB,AH=HD,
∴FH∥BD,FH=$\frac{1}{2}$BD,
∵AE=BD,AE⊥BD,
∴FQ=FH,FQ⊥FH.
(3)∵FQ=(1-$\frac{1}{x+2}$)÷$\frac{{x}^{2}+2x+1}{x+2}$=$\frac{x+1}{x+2}$•$\frac{x+2}{(x+1)^{2}}$=$\frac{1}{x+1}$,
∵x=$\sqrt{3}$-1,
∴FQ=$\frac{\sqrt{3}}{3}$,
由(2)可知,△FQH是等腰直角三角形,
∴FQ=FH=$\frac{\sqrt{3}}{3}$,QH=$\frac{\sqrt{6}}{3}$,
∴△FQH的周长=$\frac{2\sqrt{3}+\sqrt{6}}{3}$.
点评 本题考查全等三角形的判定和性质、三角形中位线定理、分式的混合运算、等腰直角三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,灵活应用三角形中位线定理,属于中考常考题型


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=120°,则∠E的度数为( )
如图,△ABC,∠ABC、∠ACB的三等分线交于点E、D,若∠BFC=132°,∠BGC=120°,则∠E的度数为( )| A. | 102° | B. | 104° | C. | 106° | D. | 108° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<y2<y3 | B. | y1>y3>y2 | C. | y1>y2>y3 | D. | y2>y3>y1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com