
����Ŀ����ͼ��������A��B�����Ӧ���������ֱ�ΪxA����5��xB��6������P�ӵ�A��������ÿ��1����λ���ٶ���������A��B֮�������˶���ͬʱ����Q�ӵ�B��������ÿ��2����λ���ٶ���������B��A֮�������˶������˶�ʱ��Ϊt�룮
(1)��t��2ʱ����P��Ӧ��������xP��______��PQ��______��
(2)��0��t��11ʱ����ԭ��Oǡ�����߶�PQ���е㣬��t��ֵ��
(3)���ǰ������ϵ�������Ӧ�ĵ��Ϊ�����㡱����P��Q�����һ�������㴦�غ�ʱ��ֱ��д���������Ӧ������
![]()
���𰸡�(1)��3��5��(2)t��1��7��(3)6.
��������
��1�������P,Q��Ӧ����������PQ��ֵ����2���������ٵ�0��t��5.5ʱ����Q�˶���δ����A����AP��t��BQ��2t����ʱOP��|5��t|��OQ��|6��2t|���ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷���Ҫʹԭ��Oǡ�����߶�PQ���е㣬��Q����λ��ԭ��O��ࣻ�г���Ӧ���̼��ɣ���3��������������t: �ٵ�0��t��5.5ʱ����Q�˶���δ����A����P��Q�����غ�ʱ��P��Q�������ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷�����P��Q�����غ�ʱ����Q�ϵ�P��AQ��AP.
�⣺(1)��t��2ʱ����P��Ӧ��������xP����5+1��2����3��
��Q��Ӧ��������xQ��6��2��2��2��
��PQ��2��(��3)��5��
�ʴ�Ϊ��3��5��
(2)��xA����5��xB��6��
��OA��5��OB��6��
�������֪����0��t��11ʱ����P�˶�����Զ·��Ϊ�����ϴӵ�A����B����Q�˶�����Զ·��Ϊ�����ϴӵ�B����A�����۷��ص���B��
���ڵ�P����Ϊ�����˶��ٶ�vP��1����P�ӵ�A�˶�����O��Ҫ5�룬�˶�����B��Ҫ11�룮
���ڵ�Q����Ϊ�����˶��ٶ�vQ��2����Q�ӵ�B�˶�����O��Ҫ3�룬�˶�����A��Ҫ5.5�룬���ص���B��Ҫ11�룮
Ҫʹԭ��Oǡ�����߶�PQ���е㣬��ҪP��Q����ֱ���ԭ��O�����࣬��OP��OQ����ʱt��5.5��
�ٵ�0��t��5.5ʱ����Q�˶���δ����A����AP��t��BQ��2t��
��ʱOP��|5��t|��OQ��|6��2t|��
��ԭ��Oǡ�����߶�PQ���е㣬
��OP��OQ��
��|5��t|��|6��2t|��
���t��1��t��![]() ��
��
���飺��t��![]() ʱ��P��Q�����غϣ��Ҷ���ԭ��O��࣬����������ȥ��t��1�������⣮
ʱ��P��Q�����غϣ��Ҷ���ԭ��O��࣬����������ȥ��t��1�������⣮
��t��1��
�ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷���Ҫʹԭ��Oǡ�����߶�PQ���е㣬��Q����λ��ԭ��O��࣬��ʱP��Q����Ĵ���λ������ͼ��ʾ��
![]()
��ʱ��OP��AP��OA��t��5��OQ��OA��AQ��5��2(t��5.5)��16��2t��
��ԭ��Oǡ�����߶�PQ���е㣬
��OP��OQ��
��t��5��16��2t��
���t��7��
���飺��t��7ʱ�������⣮
��t��7��
���Ͽ�֪��t��1��7��
(3)�ٵ�0��t��5.5ʱ����Q�˶���δ����A����P��Q�����غ�ʱ��P��Q��������ʱ��Ҫ��ʱ��Ϊ��![]() �룬
�룬
�������Ӧ����Ϊ��5+![]() ����
����![]() ���������㣬����������ȥ��
���������㣬����������ȥ��
�ڵ�5.5��t��11ʱ����P��������ԭ���Ҳ࣬��Q�Ѿ�������BA�����˶�����A���۷�����P��Q�����غ�ʱ����Q�ϵ�P��AQ��AP��
2(t��5.5)��t�����t��11��
�����Ӧ����Ϊ��5+11��6��
�ʵ�P��Q�����һ�������㴦�غ�ʱ���������Ӧ����Ϊ6��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ� �����ˣ��ҵĹ���
���������й�����ŵIJ����ӿ죬�����羭�õ��ں϶�������ߣ��й������ȶ����������羭�ø��յ���Ҫ��������ʮ���塱ʱ�ڣ�����2010����Ԫ����ۼ��㣬�й������羭����������������ʴﵽ30.5%��Ծ��ȫ���һ���롰ʮ�塱�͡�ʮһ�塱ʱ��14.2%�������������ȣ����16.3���ٷֵ㣬ͬ��������ŷԪ���ֱ�Ϊ17.8%��4.4%�������������2011��2012��2013��2014��2015�꣬�й������羭�������Ĺ����ʷֱ�Ϊ28.6%��31.7%��32.5%��29.7%��30.0%���������ֱ�Ϊ11.8%��20.4%��15.2%��19.6%��21.9%��
2016�꣬�й������羭�������Ĺ������Ծ���λ��Ԥ��ȫ�꾭������Ϊ6.7%���ң�����������Ԥ��ȫ������Ϊ2.4%���ң���2010����Ԫ����ۼ��㣬2016���й������羭�������Ĺ�������Ȼ�ﵽ33.2%���������2015��۸���㣬���й������羭�������Ĺ����ʻ����һ�㣬�����йع�����֯Ԥ�⣬2016���й����������ձ��������ٷֱ�Ϊ6.7%��1.6%��0.6%��
�������ϲ��Ͻ���������⣺
��1��ѡ����ʵ�ͳ��ͼ��ͳ�Ʊ���2013����2015���й������������羭�������Ĺ����ʱ�ʾ������
��2���������������Ϣ��2016���й��������ٴ�Լ��ȫ�����ٵ���������1λС������
��3���������������Ϣ��Ԥ��2017���й������羭�������Ĺ�����ԼΪ �� ���Ԥ�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���У���ȷ����( )
A. ƽ���ڣ�û�й�����������߶�ƽ��
B. ƽ���ڣ�û�й��������������ƽ��
C. û�й����������ֱ����ƽ��
D. ����ƽ�е�����ֱ��û�й�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
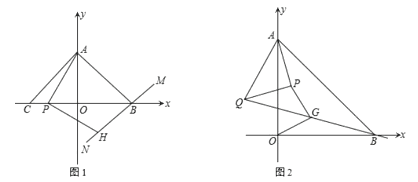
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��0��a����B��b��0����C��c��0������![]() ��0��
��0��
(1)ֱ��д�� A��B��C ��������꣺A_______��B__________��C_____��
(2)�� B ��ֱ�� MN��AB��P Ϊ�߶� OC �ϵ�һ���㣬AP��PH ��ֱ�� MN �ڵ� H��֤����PA��PH��
(3)�ڣ�1���������£����ڵ� A ����һ������ Rt��APQ �Ƶ� A ��ת���� AP��PQ����APQ��90�㣬���� BQ���� G Ϊ BQ ���е㣬�Բ����߶� OG ���߶� PG ��������ϵ��λ�ù�ϵ����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
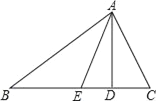
����Ŀ����ͼ��AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ���B��30�㣬��C��70�㣬�ֱ���
��1����BAC�Ķ�����
��2����AED�Ķ�����
��3����EAD�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�ֱ��y=kx+b��k��0����˫����y= ![]() �ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C��
�ཻ�ڵ�A��m��3����B����6��n������x�ύ�ڵ�C�� 
��1����ֱ��y=kx+b��k��0���Ľ���ʽ��
��2������P��x���ϣ���S��ACP= ![]() S��BOC �� ���P�����ֱ꣨��д���������
S��BOC �� ���P�����ֱ꣨��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB=AC��DΪBC�ߵ��е㣬����D��DE��AB��DF��AC������ֱ�ΪE��F��

��1����֤��DE=DF��
��2������A=60�㣬BE=1�����ABC���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=��m+2��x2��2��m+2��x��m+5������m+2��0��
��1����ö��κ����ĶԳ��᷽�̣�
��2��������C��0��n����ֱ��l��y�ᣮ �ٵ�ֱ��l��������ֻ��һ��������ʱ����n��m�ĺ�����ϵ��
������������x�����������㣬����������x���·��IJ�����x�ᷭ�ۣ�ͼ������ಿ�ֱ��ֲ��䣬�õ�һ���µ�ͼ��n=7ʱ��ֱ��l���µ�ͼ��ǡ�������������㣬���ʱm��ֵ��
��3��������ÿһ��������x��ֵ��������Ӧ�ĺ���ֵ����С��1����m��ȡֵ��Χ�� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ŶԱ���ƽ�е�ֽ��,�۳���ͼ��ʾ,EF���ۺ�,����EFB=32��,�����н�����ȷ����( )

(1)��C��EF=32��;(2)��AEC=148��;(3)��BGE=64��;(4)��BFD=116��.
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com