
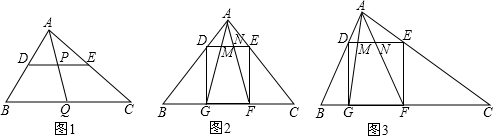
分析 (1)可证明△ADP∽△ABQ,△ACQ∽△ADP,从而根据等比代换,得出$\frac{DP}{BQ}$=$\frac{PE}{QC}$;
(2)根据三角形的面积公式求出BC边上的高$\frac{\sqrt{2}}{2}$,根据△ADE∽△ABC,求出正方形DEFG的边长$\frac{\sqrt{2}}{3}$,根据$\frac{MN}{GF}$等于高之比,即可求出MN;
(3)可得出△BGD∽△EFC,则DG•EF=CF•BG;又由DG=GF=EF,得GF2=CF•BG,再根据(1)$\frac{DM}{BG}$=$\frac{MN}{GF}$=$\frac{EN}{FC}$,从而得出答案.
解答 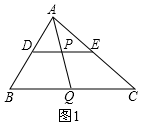 解:(1)如图1,∵DP∥BQ,
解:(1)如图1,∵DP∥BQ,
∴△ADP∽△ABQ,
∴$\frac{DP}{BQ}$=$\frac{AP}{AQ}$,
同理可得△ACQ∽△APE,
∴$\frac{EP}{CQ}$=$\frac{AP}{AQ}$,
∴$\frac{DP}{BQ}$=$\frac{EP}{CQ}$.
故答案为:∽,$\frac{AP}{AQ}$;
(2)如图2所示,作AQ⊥BC于点Q.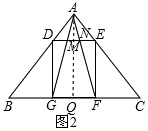
∵BC边上的高AQ=$\frac{\sqrt{2}}{2}$,
∵DE=DG=GF=EF=BG=CF,
∴DE:BC=1:3,
又∵DE∥BC,
∴AD:AB=1:3,
∴AD=$\frac{1}{3}$,DE=$\frac{\sqrt{2}}{3}$,
∵DE边上的高为$\frac{\sqrt{2}}{6}$,MN:GF=$\frac{\sqrt{2}}{6}$:$\frac{\sqrt{2}}{2}$,
∴MN:$\frac{\sqrt{2}}{3}$=$\frac{\sqrt{2}}{6}$:$\frac{\sqrt{2}}{2}$,
∴MN=$\frac{\sqrt{2}}{9}$.
故答案为:$\frac{\sqrt{2}}{9}$.
(3)证明:如图3,∵∠B+∠C=90°∠CEF+∠C=90°,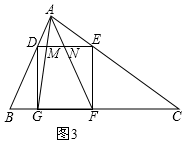
∴∠B=∠CEF,
又∵∠BGD=∠EFC,
∴△BGD∽△EFC,
∴$\frac{DG}{CF}$=$\frac{BG}{EF}$,
∴DG•EF=CF•BG,
又∵DG=GF=EF,
∴GF2=CF•BG,
由(1)得$\frac{DM}{BG}$=$\frac{MN}{GF}$=$\frac{EN}{FC}$,
∴$\frac{MN}{GF}$×$\frac{MN}{GF}$=$\frac{DM}{BG}$×$\frac{EN}{CF}$,
∴($\frac{MN}{GF}$)2=$\frac{DM}{BG}$×$\frac{EN}{CF}$,
∵GF2=CF•BG,
∴MN2=DM•EN.
点评 本题属于相似形综合题,主要考查了相似三角形的判定和性质以及正方形的性质的综合应用,解决问题的关键是运用相似三角形的性质列出比例式进行推导计算.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形或作辅助线构造相似三角形.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
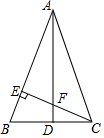 如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E,BE=2,BC=6.
如图,在△ABC中,AB=AC,BD=CD,CE⊥AB于E,BE=2,BC=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
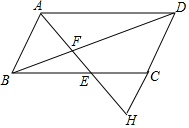 如图,点H在平行四边形ABCD的边DC延长线上,连结AH分别交BC、BD于点E、F.求证:$\frac{BE}{AD}$=$\frac{AB}{DH}$.
如图,点H在平行四边形ABCD的边DC延长线上,连结AH分别交BC、BD于点E、F.求证:$\frac{BE}{AD}$=$\frac{AB}{DH}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | |
| 甲种车辆数单位(辆) | 2 | 5 |
| 乙种车辆数单位(辆) | 3 | 6 |
| 累计运货数单位(吨) | 15.5 | 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com