
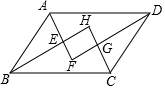
 如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件).
如图,在?ABCD中,AF、BH、CH、DF分别是∠DAB、∠ABC、∠BCD、∠CDA的平分线,AF与BH交于点E,CH与DF交于点G.在不添加其他条件的情况下,试写出上述条件推出的结论,并选择你喜欢的一个结论说明成立的理由.(要求推理过程中用到″平行四边形″和″角平分线″这两个条件). 分析 可推出:AE⊥BE.根据在平行四边形中邻角互补,有∠DAB+∠ABC=180°.再根据角的平分线的性质有,∠EAB+∠EBA=$\frac{1}{2}$(∠DAB+∠ABC),可推出∠AEB=90°,即AE⊥BE.
解答 解:结论:AE⊥BE,BH⊥CH,CG⊥DG,AF⊥DF,四边形EFGH是矩形,△ABE≌△CDG,△BCH≌△DAF;
:在?ABCD中,∵AD∥BC,
∴∠DAB+∠ABC=180°.
∵AE,BE分别平分∠DAB,∠ABC,
∴∠EAB+∠EBA=$\frac{1}{2}$(∠DAB+∠ABC)=$\frac{1}{2}$×180°=90°.
∴∠AEB=90°,
∴AE⊥BE.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质;本题是开放题,答案不唯一,利用平行四边形的性质和角的平分线的性质推理求解.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5(x+1)=5.7 | B. | 5.7(x-1)=5 | C. | 5(x+1)2=5.7 | D. | 5+5x=5.7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
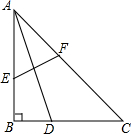 如图,在△ABC中,∠B=90°,AB=BC=6,把△ABC进行折叠,使点A与点D复合,BD:DC=1:2,折痕为EF,点E在AB上,点F在AC上,求EC的长.
如图,在△ABC中,∠B=90°,AB=BC=6,把△ABC进行折叠,使点A与点D复合,BD:DC=1:2,折痕为EF,点E在AB上,点F在AC上,求EC的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com