
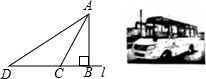
 如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.
如图是我市投入使用的“大鼻子”校车,其安全隐患主要是超速和超载,某中学九年级数学活动小组设计了如下检测公路上行驶汽车速度的实验,先在笔直的车道l旁边选取一点A,再在l上确定点B,使AB⊥l,测得AB的长为30米,又在l上选取点C,D,使∠CAB=30°,∠DAB=60°,如图所示.分析 (1)分别在Rt△ADB与Rt△ACB中,利用正切函数,即可求得DB与BC的长,继而求得CD的长;
(2)由从C到D用时3秒,即可求得这辆校车的速度,比较与40千米/小时的大小,即可确定这辆校车是否超速.
解答 解:(1)由題意得,
在Rt△ADB中,AB=30米,
∴BD=$\frac{AB}{tan30°}$=30$\sqrt{3}$=51.9(米),
在Rt△ABC中,BC=$\frac{AB}{tan60°}$=10$\sqrt{3}$=17.3(米),
则CD=BD-BC=51.9-17.3=34.6(米);
(2)超速.
理由:∵汽车从C到D用时3秒,
∴校车速度为34.6÷3×3.6≈41.52(千米/小时),
∵41.52>40,
∴此校车在CD路段超速.
点评 此题考查了解直角三角形的应用问题.此题难度适中,解题的关键是把实际问题转化为数学问题求解,是中考常见题型.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
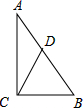 如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )
如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线,那么下列结论错误的是( )| A. | ∠A+∠DCB=90° | B. | ∠ADC=2∠B | C. | AB=2CD | D. | BC=CD |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ①②③④ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
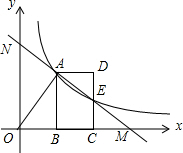 如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).
如图,O为原点,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,作AB⊥x轴于点B,点A的坐标为(2,3).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
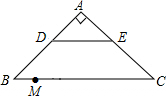 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是$\frac{25}{6}$或$\frac{50}{13}$.
如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是$\frac{25}{6}$或$\frac{50}{13}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com