
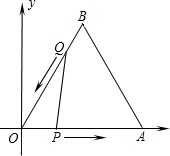
 如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:
如图,等边△ABO放置在平面直角坐标系中,OA=4,动点P、Q同时从O、B两点出发,分别沿OA、BO方向匀速运动,它们的速度均为每秒1个单位长度,当点P到达点A时,P、Q两点停止运动,设点P的运动时间为x(s)(0<x<4),解答下列问题:分析 (1)过点Q作QD⊥OA于点D,解直角三角形QOD,分别求出OD,QD和x的关系式,即可得到点Q的坐标;
(2)由三角形面积公式可得s与x之间的二次函数关系式,然后利用配方法求得其最大值即可;
(3)存在某个时刻x的值,使△OPQ的面积为$\frac{3\sqrt{3}}{4}$个平方单位,由(2)可知把y=$\frac{3\sqrt{3}}{4}$代入求出对应的x值即可.
解答 解:
(1)过点Q作QD⊥OA于点D,如图所示:
∵△ABO是等边三角形,
∴∠AOB=60°,
∵动点Q从B点出发,速度为每秒1个单位长度,
∴BQ=x,
∴OQ=4-x,
在Rt△QOD中,OD=OQ•cos60°=(4-x)×$\frac{1}{2}$=2-$\frac{1}{2}$x,
QD=OQ•sin60°=(4-x)×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x,
∴点Q的坐标为(2-$\frac{1}{2}$x,2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x);
(2)∵动点P从O点出发,速度为每秒1个单位长度,
∴OP=x,
∴S=$\frac{1}{2}$OP•QD=$\frac{1}{2}$x(2$\sqrt{3}$-$\frac{\sqrt{3}}{2}$x)=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x,
=-$\frac{\sqrt{3}}{4}$(x-2)2+$\sqrt{3}$(0<x<4),
∵a=-$\frac{\sqrt{3}}{4}$<0,
∴当x=2时,S有最大值,最大值为$\sqrt{3}$;
(3)存在某个时刻x的值,使△OPQ的面积为$\frac{3\sqrt{3}}{4}$个平方单位,理由如下:,
假设存在某个时刻,使△OPQ的面积为$\frac{3\sqrt{3}}{4}$个平方单位,
由(2)可知)=-$\frac{\sqrt{3}}{4}$x2+$\sqrt{3}$x=$\frac{3\sqrt{3}}{4}$,
解得x=1或x=3,
∵0<x<4,
∴x=1或x=3都成了,
即当x=1s或3s时,能使△OPQ的面积为$\frac{3\sqrt{3}}{4}$个平方单位.
点评 本题主要考查了和三角形有关的知识,其中用到了二次函数的最值、等边三角形的性质、特殊角的锐角的锐角三角函数值、解一元二次方程、图形面积的求法,题目的综合性较强,对学生的计算能力要求很高,是一道不错的中考压轴题目.


科目:初中数学 来源: 题型:填空题
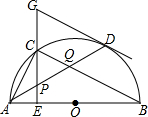 如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:
如图,AB是半圆O的直径,D是$\widehat{AB}$上一点,C是$\widehat{AD}$的中点,过点C作AB的垂线,交AB于E,与过点D的切线交于点G,连接AD,分别交CE、CB于点P、Q,连接AC,关于下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
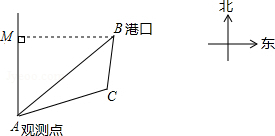 已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10$\sqrt{2}$km,一艘货轮从B港口沿如图所示的BC方向航行4$\sqrt{7}$km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.
已知B港口位于A观测点北偏东45°方向,且其到A观测点正北风向的距离BM的长为10$\sqrt{2}$km,一艘货轮从B港口沿如图所示的BC方向航行4$\sqrt{7}$km到达C处,测得C处位于A观测点北偏东75°方向,则此时货轮与A观测点之间的距离AC的长为( )km.| A. | 8$\sqrt{3}$ | B. | 9$\sqrt{3}$ | C. | 6$\sqrt{3}$ | D. | 7$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.
在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-1(m>0)与x轴的交点为A,B.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com