
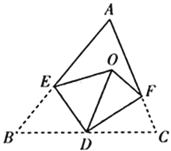
【题目】如图,已知点![]() ,
,![]() ,
,![]() 分别在
分别在![]() 的三边上,将
的三边上,将![]() 沿
沿![]() ,
,![]() 翻折,顶点
翻折,顶点![]() ,
,![]() 均落在
均落在![]() 内的点
内的点![]() 处,且
处,且![]() 与
与![]() 重合于线段
重合于线段![]() ,若
,若![]() ,则
,则![]() 的度数为( )
的度数为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接CO、BO.由题意DO=DB=DC,推出∠AOC=90°,∠OBC+∠OCB=90°,由EO=EB,FO=FC,推出∠EBO=∠EOB,∠FOC=∠FCO,推出∠AEO=2∠EBO,∠AFO=2∠FCO,由∠AEO+∠AFO=58°,推出∠EBO +∠FCO =29°,由此即可解决问题.
如图,连接CO、BO.

根据折叠的性质得:DB=DC=DO,
∴∠BOC=90°,∠OBC+∠OCB=90°,
根据折叠的性质得:EO=EB,FO=FC,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴∠AEO=2∠EBO,∠AFO=2∠FCO,
∵∠AEO +∠AFO =58°,
∴2∠EBO +2∠FCO =58°,
∴∠EBO +∠FCO =29°,
∴∠ABC+∠ACB=∠EBO +∠OBC+∠OCB+∠FCO=90°+29°=119°,
∴∠A=180°-(∠ABC+∠ACB)=180°-119°=61°,
故选:D.


科目:初中数学 来源: 题型:
【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式 | 支付宝 | 微信 | 其他 |
人数/人 |
| 200 | 75 |
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电脑公司销售部为了定制下个月的销售计划,对20位销售员本月的销售量进行了统计,绘制成如图所示的统计图,则这20位销售人员本月销售量的平均数、中位数、众数分别是( )
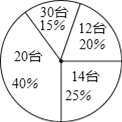
A. 19,20,14 B. 19,20,20 C. 18.4,20,20 D. 18.4,25,20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电视机厂要印制产品宣传材料甲印刷厂提出:每份材料收1元印制费,另需收取所有印制材料的制版费1500元;乙印刷厂提出:每份材料收2.5元印制费,不收制版费.设该电视厂在同一个印刷厂一次印的数量为![]() 份
份![]() .
.
(1)根据题意填表:
一次印制数量(份) | 300 | 500 | 1500 | … |
甲印刷厂花费(元) | 2000 | … | ||
乙印刷厂花费(元) | 1250 | … |
(2)设在甲印刷厂花费![]() 元,在乙印刷厂花费
元,在乙印刷厂花费![]() 元,分别求
元,分别求![]() ,
,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)根据题意填空:
①若电视厂在甲印刷厂和在乙印刷厂一次印制宣传材料的数量相同,且花费相同,则该电视厂在同一个印刷厂一次印制材料的数量为 份;
②印制800份宣传材料时,选择 印刷厂比较合算;
③电视机厂拟拿出3000元用于印制宣传材料,在 印刷厂印制宣传材料可以多一些.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,网格中每个小正方形的边长均为1,线段AB、线段EF的端点均在小正方形的顶点上.
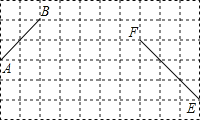
(1)在图中以AB为边画Rt△BAC,点C在小正方形的顶点上,使∠BAC=90°,tan∠ACB=![]() ;
;
(2)在(1)的条件下,在图中画以EF为边且面积为3的△DEF,点D在小正方形的顶点上,连接CD、BD,使△BDC是锐角等腰三角形,直接写出∠DBC的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列内容,并解决问题.
一道习题引发的思考
小明在学习《勾股定理》一章内容时,遇到了一个习题,并对有关内容进行了研究;
习题再现:
古希腊的哲学家柏拉图曾指出,如果![]() 表示大于1的整数,
表示大于1的整数,![]() ,
,![]() ,
,![]() ,那么
,那么![]() ,
,![]() ,
,![]() 为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
为勾股数.你认为对吗?如果对,你能利用这个结论得出一些勾股数吗?
资料搜集:
定义:勾股数是指可以构成一个直角三角形三边的一组正整数.一般地,若三角形三边长![]() ,
,![]() ,
,![]() 都是正整数,且满足
都是正整数,且满足![]() ,那么
,那么![]() ,
,![]() ,
,![]() 称为一组勾股数.
称为一组勾股数.
关于勾股数的研究:我囯西周初数学家商高在公元前1000年发现了“勾三,股四,弦五”,这组数![]() 是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:
是世界上最早发现的一组勾股效,毕达哥拉斯学派、柏拉图学派、我国数学家刘徽、古希腊数学家丢番图都进行过勾股数的研究.习题中的表达式是柏拉图给出的勾股数公式,这个表达式未给出全部勾股数,世界上第一次给出勾股数通解公式的是《九幸算术),其勾股数公式为:![]() ,
,![]() ,
,![]()
![]() ,其中
,其中![]() ,
,![]() ,
,![]() 是互质的奇数.(注:
是互质的奇数.(注:![]() ,
,![]() ,
,![]() 的相同倍数组成的一组数也是勾股数)
的相同倍数组成的一组数也是勾股数)

问题解答:
(1)根据柏拉图的研究,当![]() 时,请直接写出一组勾股数;
时,请直接写出一组勾股数;
(2)若![]() 表示大于1的整数,试证明
表示大于1的整数,试证明![]() 是一组勾股数;
是一组勾股数;
(3)请举出一个反例(即写出一组勾股数),说明柏拉图给出的勾股数公式不能构造出所有的勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,点
,点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() 的坐标为
的坐标为![]() ,将线段
,将线段![]() 沿
沿![]() 轴的正方向平移
轴的正方向平移![]() 个单位后得到线段
个单位后得到线段![]() .
.
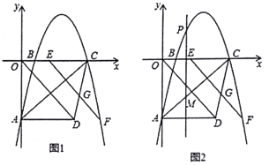
(1)当![]() ______时,点
______时,点![]() 或点
或点![]() 正好移动到抛物线上;
正好移动到抛物线上;
(2)当点![]() 正好移动到抛物线上,
正好移动到抛物线上,![]() 与
与![]() 相交于点
相交于点![]() 时,求
时,求![]() 点坐标;
点坐标;
(3)如图2,若点![]() 是
是![]() 轴上方抛物线上一动点,过点
轴上方抛物线上一动点,过点![]() 作平行于
作平行于![]() 轴的直线交
轴的直线交![]() 于点
于点![]() ,探索是否存在点
,探索是否存在点![]() ,使线段
,使线段![]() 长度有最大值?若存在,直接写出点
长度有最大值?若存在,直接写出点![]() 的坐标和
的坐标和![]() 长度的最大值;若不存在,请说明理由.
长度的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图1所示的圆心角为![]() 的扇形上,将一根橡皮筋(可伸缩)的一端固定在一个位置,拉直橡皮筋,将它的另一端沿
的扇形上,将一根橡皮筋(可伸缩)的一端固定在一个位置,拉直橡皮筋,将它的另一端沿![]() 匀速移动,从点
匀速移动,从点![]() 出发,沿箭头所示的方向经过点
出发,沿箭头所示的方向经过点![]() 再沿着
再沿着![]() 走到点
走到点![]() .设移动过程中橡皮筋的长度为
.设移动过程中橡皮筋的长度为![]() (单位:米),表示
(单位:米),表示![]() 与移动路程
与移动路程![]() 的函数关系的图象大致如图2,则这个固定位置可能是图1中的( )
的函数关系的图象大致如图2,则这个固定位置可能是图1中的( )
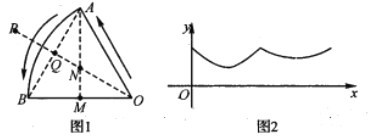
A.点![]() B.点
B.点![]() C.点
C.点![]() D.点
D.点![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com