
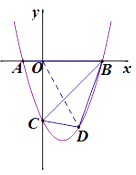
”¾ĢāÄæ”æČēĶ¼£Ø1£©£¬Å×ĪļĻßy=ax2+bx+cÓėxÖį½»ÓŚA£Øx1,0£©”¢B£Øx2,0£©Į½µć£Øx1<0<x2£©£¬ÓėyÖį½»ÓŚµćC(0,-3),ČōÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=1,ĒŅtan”ĻOAC=3.
£Ø1£©ĒóÅ×ĪļĻßµÄŗÆŹż½āĪöŹ½£»
£Ø2£©ČōµćDŹĒÅ×ĪļĻßBC¶ĪÉĻµÄ¶Æµć£¬ĒŅµćDµ½Ö±ĻßBC¾ąĄėĪŖ ![]() £¬ĒóµćDµÄ×ų±ź
£¬ĒóµćDµÄ×ų±ź
£Ø3£©ČēĶ¼£Ø2£©£¬ČōÖ±Ļßy=mx+n¾¹żµćA,½»yÖįÓŚµćE(0, £ ![]() ),µćPŹĒÖ±ĻßAEĻĀ·½Å×ĪļĻßÉĻŅ»µć£¬¹żµćP×÷xÖįµÄ“¹Ļß½»Ö±ĻßAEÓŚµćM,µćNŌŚĻ߶ĪAMŃÓ³¤ĻßÉĻ£¬ĒŅPM=PN,ŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PMNµÄÖܳ¤ÓŠ×ī“óÖµ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź¼°”÷PMNµÄÖܳ¤µÄ×ī“óÖµ£»Čō²»“ęŌŚ,ĒėĖµĆ÷ĄķÓÉ.
),µćPŹĒÖ±ĻßAEĻĀ·½Å×ĪļĻßÉĻŅ»µć£¬¹żµćP×÷xÖįµÄ“¹Ļß½»Ö±ĻßAEÓŚµćM,µćNŌŚĻ߶ĪAMŃÓ³¤ĻßÉĻ£¬ĒŅPM=PN,ŹĒ·ń“ęŌŚµćP£¬Ź¹”÷PMNµÄÖܳ¤ÓŠ×ī“óÖµ£æČō“ęŌŚ£¬Ēó³öµćPµÄ×ų±ź¼°”÷PMNµÄÖܳ¤µÄ×ī“óÖµ£»Čō²»“ęŌŚ,ĒėĖµĆ÷ĄķÓÉ.
”¾“š°ø”æ
£Ø1£©
ŌŚRt”÷AOCÖŠ£¬tan ![]() OAC=
OAC= ![]() =3£¬ĒŅOC=3£¬
=3£¬ĒŅOC=3£¬
”ąOA=1£¬A£Ø-1£¬0£©
”ßÅ×ĪļĻߵĶŌ³ĘÖįĪŖÖ±Ļßx=1
”ąÓÉÖŠµć×ų±ź¹«Ź½æÉĒó£ŗ ![]() £¬½āµĆx=3
£¬½āµĆx=3
”ąB£Ø3£¬0£©
”ąæÉÉčÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗy=a£Øx-3£©£Øx+1£©
½«C£Ø0£¬-3£©“śČėÉĻŹ½ÖŠ£¬a”Į£Ø-3£©=-3£¬
½āµĆ£ŗa=1
”ąÅ×ĪļĻߵıķ“ļŹ½ĪŖ£ŗy=£Øx-3£©£Øx+1£©=x2-2x-3
£Ø2£©
”ßB£Ø3£¬0£©”¢C£Ø0£¬-3£©
”ą ![]()
”ą ![]()
ÉčD£Øx£¬x2-2x-3£©.Į¬½ÓOD.
”ą ![]()
= ![]()
= ![]()
= ![]()
=3
½āµĆ£ŗx1=1£¬x2=2
”ąD£Ø1£¬-4£©£Ø2£¬-3£©
£Ø3£©
ÓÉA£Ø-1,0£©”¢E£Ø0£¬- ![]() £©æÉĒó£ŗ
£©æÉĒó£ŗ
Ö±ĻßAEµÄ±ķ“ļŹ½ĪŖ£ŗy= ![]() £¬AE=
£¬AE= ![]()
Éčp£Øt£¬t2-2t-3£©£¬ŌņM£Øt£¬ ![]() t
t ![]() £©
£©
”ąPM= ![]() t
t ![]() -£Øt2-2t-3£©=- t2+
-£Øt2-2t-3£©=- t2+ ![]()
×÷PG”ĶMNÓŚG£¬
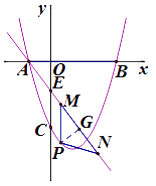
ÓÉPM=PNµĆ£ŗMG=NG= ![]() MN
MN
ÓÉ”÷PMG”×”÷AEOÓŠ£ŗ ![]() £¬¼“
£¬¼“ ![]()
”ąMG= ![]() PM=NG
PM=NG
”ąC”÷PMN=PM+PN+MN= ![]() PM=
PM= ![]() £Ø- t2+
£Ø- t2+ ![]() £©=-
£©=- ![]() t2+
t2+ ![]() t+6
t+6
”ąµ±t= ![]() Ź±£¬C”÷PMNÓŠ×ī“óÖµĪŖ
Ź±£¬C”÷PMNÓŠ×ī“óÖµĪŖ ![]() £¬“ĖŹ±P
£¬“ĖŹ±P ![]()
”¾½āĪö”æ£Ø1£©CµćµÄ×ų±źŅŃÖŖ£¬tan”ĻOAC£¬¾Ż“ĖĒó³öAµć×ų±ź£»¶Ō³ĘÖįŹĒx=1£¬¾Ż“ĖĒó³öBµć×ų±ź”££Ø2£©B”¢CĮ½µćµÄ×ų±źŹĒŅŃÖŖ£¬øł¾ŻĮ½µćÖ®¼äµÄ¾ąĄė¹«Ź½Ēó³öBCµÄ³¤¶Č£¬µćDµ½Ö±ĻßBCµÄ¾ąĄėĪŖ ![]() £¬øł¾Ż
£¬øł¾Ż ![]() BCDµÄĆ껿Ēó³öDµćµÄ×ų±ź”££Ø3£©ŅŃÖŖA”¢EĮ½µćµÄ×ų±ź£¬æÉŅŌĻČĒó³öÖ±ĻßAEµÄ±ķ“ļŹ½”£Ņ×ÖŖP”¢MµÄŗį×ų±źĻąĶ¬£¬·Ö±šÉč³öP”¢MĮ½µć”£ÓĆPM·Ö±š±ķŹ¾³öPN£¬MN£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬Ēó³ö
BCDµÄĆ껿Ēó³öDµćµÄ×ų±ź”££Ø3£©ŅŃÖŖA”¢EĮ½µćµÄ×ų±ź£¬æÉŅŌĻČĒó³öÖ±ĻßAEµÄ±ķ“ļŹ½”£Ņ×ÖŖP”¢MµÄŗį×ų±źĻąĶ¬£¬·Ö±šÉč³öP”¢MĮ½µć”£ÓĆPM·Ö±š±ķŹ¾³öPN£¬MN£¬øł¾Ż¶ž“ĪŗÆŹżµÄŠŌÖŹ£¬Ēó³ö ![]() PMNÖܳ¤µÄ×ī“óÖµ¼°“ĖŹ±PµćµÄ×ų±ź”£
PMNÖܳ¤µÄ×ī“óÖµ¼°“ĖŹ±PµćµÄ×ų±ź”£
”¾æ¼µć¾«Īö”æ±¾ĢāÖ÷ŅŖæ¼²éĮĖ¶ž“ĪŗÆŹżµÄĶ¼ĻóŗĶ¶ž“ĪŗÆŹżµÄŠŌÖŹµÄĻą¹ŲÖŖŹ¶µć£¬ŠčŅŖÕĘĪÕ¶ž“ĪŗÆŹżĶ¼Ļń¹Ų¼üµć£ŗ1”¢æŖæŚ·½Ļņ2”¢¶Ō³ĘÖį 3”¢¶„µć 4”¢ÓėxÖį½»µć 5”¢ÓėyÖį½»µć£»Ōö¼õŠŌ£ŗµ±a>0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ų¼õŠ”£»¶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ųŌö“ó£»µ±a<0Ź±£¬¶Ō³ĘÖį×ó±ß£¬yĖęxŌö“ó¶ųŌö“󣻶Ō³ĘÖįÓŅ±ß£¬yĖęxŌö“ó¶ų¼õŠ”²ÅÄÜÕżČ·½ā“š“ĖĢā£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ£Ø1£©ÓŠĄķŹż![]() ŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬ĒŅ
ŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬ĒŅ![]() £¬»Æ¼ņ£ŗ
£¬»Æ¼ņ£ŗ![]() £®
£®
![]() ””
””
£Ø2£©£®ŅŃÖŖ![]() ŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬»Æ¼ņ£ŗ
ŌŚŹżÖįÉĻµÄĪ»ÖĆČēĶ¼ĖłŹ¾£¬»Æ¼ņ£ŗ![]() £®
£®
![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖA£¬BŌŚŹżÖįÉĻ±ķŹ¾µÄŹż·Ö±šŹĒm£¬n.
£Ø1£©ĢīŠ“ĻĀ±ķ£ŗ

£Ø2£©ČōA£¬BĮ½µć¼äµÄ¾ąĄėĪŖd£¬Š“³ödÓėm£¬nÖ®¼äµÄŹżĮæ¹ŲĻµ.
(3)ŌŚŹżÖįÉĻ±ź³öĖłÓŠ·ūŗĻĢõ¼žµÄÕūŹżµćP£¬Ź¹Ėüµ½5ŗĶ-5µÄ¾ąĄėÖ®ŗĶĪŖ10£¬²¢Ēó³öĖłÓŠÕāŠ©ÕūŹżµÄŗĶ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĢŻŠĪÖ½Ę¬ABCDÖŠ£¬AD//BC£¬AD>CD£¬½«Ö½Ę¬ŃŲ¹żµćDµÄÖ±ĻßÕŪµž£¬Ź¹µćCĀäŌŚADÉĻµÄµćC“¦£¬ÕŪŗŪDE½»BCÓŚµćE£¬Į¬½įC”äE£®
ĒóÖ¤£ŗĖıߊĪCDC”äEŹĒĮāŠĪ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅ»“ĪŹżŃ§»ī¶ÆæĪÉĻ£¬ĄĻŹ¦ĮōĻĀĮĖÕāŃłŅ»µĄĢā”°ČĪ»Ņ»øö”÷ABC£¬ŅŌBCµÄÖŠµćOĪŖ¶Ō³ĘÖŠŠÄ£¬×÷”÷ABCµÄÖŠŠÄ¶Ō³ĘĶ¼ŠĪ£¬ĪŹ”÷ABCÓėĖüµÄÖŠŠÄ¶Ō³ĘĶ¼ŠĪĘ“³ÉĮĖŅ»øöŹ²Ć“ŠĪדµÄĢŲŹāĖıߊĪ£æ²¢ĖµĆ÷ĄķÓÉ.”±
ÓŚŹĒ“ó¼ŅĢÖĀŪæŖĮĖ£¬Š”ĮĮĖµ£ŗ”°Ę“³ÉµÄŹĒĘ½ŠŠĖıߊĪ”±£» Š”»ŖĖµ£ŗ”°Ę“³ÉµÄŹĒ¾ŲŠĪ”±£»
Š”ĒæĖµ£ŗ”°Ę“³ÉµÄŹĒĮāŠĪ”±£» Š”ŗģĖµ£ŗ”°Ę“³ÉµÄŹĒÕż·½ŠĪ”±£»ĘäĖūĶ¬Ń§Ņ²Ėµ³öĮĖ×Ō¼ŗµÄæ“·Ø””ÄćŌŽĶ¬ĖūĆĒÖŠµÄĖµÄ¹Ūµć£æĪŖŹ²Ć“£æČō¶¼²»ŌŽĶ¬£¬ĒėĖµ³öÄćµÄ¹Ūµć£Ø»³öĶ¼ŠĪ£©£¬²¢ĖµĆ÷ĄķÓÉ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚŅ»øö²»ĶøĆ÷µÄæŚ“üĄļ×°ÓŠČōøÉøöĻąĶ¬µÄŗģĒņ£¬ĪŖĮĖ¹Ą¼Ę“üÖŠŗģĒņµÄŹżĮæ£¬Ä³Ń§Ļ°Š”×é×öĮĖĆžĒņŹµŃ飬ĖūĆĒ½«30øöÓėŗģĒņ“󊔊ĪדĶźČ«ĻąĶ¬µÄ°×Ēņ×°Čė“üÖŠ£¬½ĮŌČŗó“ÓÖŠĖ껜ƞ³öŅ»øöĒņ²¢¼ĒĻĀŃÕÉ«£¬ŌŁ°ŃĖü·Å»Ų“üÖŠ£¬²»¶ĻÖŲø“£®ĻĀ±ķŹĒ¼ø“Ī»ī¶Æ»ć×ÜŗóĶ³¼ĘµÄŹż¾Ż£ŗ

£Ø1£©Ēė¹Ą¼Ę£ŗµ±“ĪŹżsŗÜ“óŹ±£¬Ćžµ½°×ĒņµÄʵĀŹ½«»į½Ó½ü”” ”” £»¼ŁČēÄćČ„ĆžŅ»“Ī£¬ÄćĆžµ½°×ĒņµÄøÅĀŹŹĒ”” ””£Ø¾«Č·µ½0.1£©£®
£Ø2£©ŹŌ¹ĄĖćæŚ“üÖŠŗģĒņÓŠ¶ąÉŁÖ»£æ
£Ø3£©½ā¾öĮĖÉĻĆęµÄĪŹĢāŗóĒėÄć“ÓĶ³¼ĘÓėøÅĀŹ·½ĆęĢøŅ»ĢõĘōŹ¾£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬”÷ABCÖŠ£¬DŹĒABµÄÖŠµć£¬EŹĒACÉĻŅ»µć£¬EF”ĪAB£¬ DF”ĪBE£®ĒėÄć²ĀĻėDFÓėAEµÄ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖµćAŌŚŹżÖįÉĻ¶ŌÓ¦µÄÓŠĄķŹżĪŖa£¬½«µćAĻņ×óŅʶÆ6øöµ„Ī»³¤¶Č£¬ŌŁĻņÓŅŅʶÆ2øöµ„Ī»³¤¶ČÓėµćBÖŲŗĻ£¬µćB¶ŌÓ¦µÄÓŠĄķŹżĪŖ©24£®
£Ø1£©Ēóa£»
£Ø2£©Čē¹ūŹżÖįÉĻµÄµćCŌŚŹżÖįÉĻŅʶÆ3øöµ„Ī»³¤¶Čŗ󣬾ąBµć8øöµ„Ī»³¤¶Č£¬ÄĒĆ“ŅʶÆĒ°µÄµćC¾ąĄėŌµćÓŠ¼øøöµ„Ī»³¤¶Č£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijÉĢ³”³ļ¼Æ׏½š12.8ĶņŌŖ£¬Ņ»“ĪŠŌ¹ŗ½ųæÕµ÷”¢²Źµē¹²30ĢØ£®øł¾ŻŹŠ³”ŠčŅŖ£¬ÕāŠ©æÕµ÷”¢²ŹµēæÉŅŌČ«²æĻśŹŪ£¬Č«²æĻśŹŪŗóĄūČó²»ÉŁÓŚ1.5ĶņŌŖ£¬ĘäÖŠæÕµ÷”¢²ŹµēµÄ½ų¼ŪŗĶŹŪ¼Ū¼ū±ķøń£®
æÕµ÷ | ²Źµē | |
½ų¼Ū£ØŌŖ/ĢØ£© | 5400 | 3500 |
ŹŪ¼Ū£ØŌŖ/ĢØ£© | 6100 | 3900 |
ÉčÉĢ³”¼Ę»®¹ŗ½ųæÕµ÷xĢØ£¬æÕµ÷ŗĶ²ŹµēČ«²æĻśŹŪŗóÉĢ³”»ńµĆµÄĄūČóĪŖyŌŖ£®
£Ø1£©ŹŌŠ“³öyÓėxµÄŗÆŹż¹ŲĻµŹ½£»
£Ø2£©ÉĢ³”ÓŠÄļøÖÖ½ų»õ·½°øæɹ©Ń”Ōń£æ
£Ø3£©Ń”ŌńÄÄÖÖ½ų»õ·½°ø£¬ÉĢ³”»ńĄū×ī“ó£æ×ī“óĄūČóŹĒ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com