
����Ŀ���ּƻ��Ѽ��ֻ���1240�ֺ����ֻ���880����һ�л�������ij�أ���֪���л�������A��B���ֲ�ͬ���Ļ����Ṳ40�ڣ�ʹ��A�ͳ���ÿ�ڷ���Ϊ6000Ԫ��ʹ��B�ͳ���ÿ�ڷ���Ϊ8000Ԫ.
��1������������������ܷ���Ϊy��Ԫ�����л�����A�ͳ���x �ڣ��Զ����ó������x��ʾ�ܷ���y�Ĺ�ʽ.
��2�����ÿ��A�ͳ�������װ���ֻ���35�ֺ����ֻ���15�֣�ÿ��B�ͳ�������װ���ֻ���25�ֺ����ֻ���35�֣�װ��ʱ����Ҫ����A��B���ֳ���Ľ�������ô�����ļ��ְ��ų���ķ�����
���𰸡�(1) y��32��0.2x;(2) �������ַ�����A��B���ֳ���Ľ����ֱ�Ϊ24�ڡ�16�ڻ�25�ڡ�15�ڻ�26�ڡ�14��
�������������������1���ܷ���=0.6��A�ͳ������+0.8��B�ͳ��������
��2��Ӧ�ֱ��ʾ���������װ�صļ������ֻ����������35��A�ͳ������+25��B�ͳ��������1240��15��A�ͳ������+35��B�ͳ��������880��
���������(1)6000Ԫ=0.6��Ԫ��8000Ԫ=0.8��Ԫ��
����A�ͳ���x��,����B�ͳ���(40x)�ڣ����˷�Ϊy��Ԫ��
������,��y=0.6x+0.8(40x)=0.2x+32��
(2)������,�� ��
��
��ã� ![]() ��
��
��24x26��
��xȡ��������A�ͳ������24�ڻ�25�ڻ�26�ڣ���Ӧ������װ��������
��24��A�ͳ����16��B�ͳ��
��25��A�ͳ����15��B�ͳ��
��26��A�ͳ����14��B�ͳ���.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx��1��a��0����ͼ���㣨1��1������a+b+1��ֵ�ǣ� ��
A.��3B.��1C.2D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=2��x��3����x��5���ĶԳ�����ֱ�ߣ�������
A.x=3B.x=5C.x=4D.x=8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����O��ֱ��AB=12��P����BC��һ���㣨���B��C���غϣ�����ABC=30�㣬����P��PD��OP����O�ڵ�D��
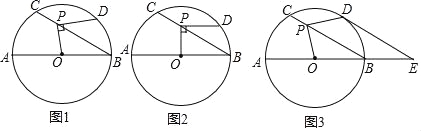
��1����ͼ2����PD��ABʱ����PD�ij���
��2����ͼ3����![]() ʱ���ӳ�AB����E��ʹBE=
ʱ���ӳ�AB����E��ʹBE=![]() AB������DE��
AB������DE��
����֤��DE����O�����ߣ�
����PC�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һɽ��ѧУΪ���ּ�Զ��ѧ������ס�ޣ������ֽ��Ҹ�������ɼ�ס��. ���ÿ��ס5�ˣ���ô��12�˰��Ų��£����ÿ��ס8�ˣ���ô��һ�䷿����һЩ��λ���ʸ�У�����м���ס��������ѧ��ס�ޣ�ס��ѧ�������ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��P��x��y����x��ľ���Ϊ2����y��ľ���Ϊ3����x+y��0��xy��0�����P������Ϊ��������
A.����2��3��B.��2��3��C.��3����2��D.��3��2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����E��AC���ӳ����ϣ��������������ж�AB��CD���ǣ� ��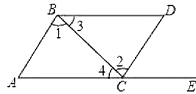
A.��3=��A
B.��l=��2
C.��D=��DCE
D.��D+��ACD=180
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com