
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯпyЃНЉx2+2x+cгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаЕуAЃЈЉ1ЃЌ0ЃЉЃЌХзЮяЯпгыyжсНЛгкЕуCЃЌЖЅЕуЮЊDЃЎ
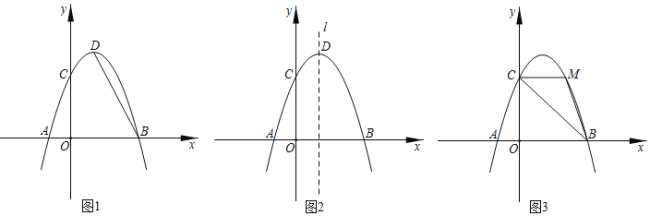
ЃЈ1ЃЉШчЭМ2ЃЌжБЯпlЪЧХзЮяЯпЕФЖдГЦжсЃЌЕуPЪЧжБЯпlЩЯвЛЖЏЕуЃЌЪЧЗёДцдкЕуPЃЌЪЙЁїPBCЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧѓЕуPЕФзјБъЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЃЈ2ЃЉШчЭМ3ЃЌСЌНгBCЃЌЕуMЪЧжБЯпBCЩЯЗНЕФХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЕБЁїMBCЕФУцЛ§зюДѓЪБЃЌЧѓЁїMBCЕФУцЛ§ЕФзюДѓжЕЃЛЕуNЪЧЯпЖЮBCЩЯЕФвЛЕуЃЌЧѓMN+![]() BNЕФзюаЁжЕЃЎ
BNЕФзюаЁжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉДцдкЃЌЕуPЕФзјБъЮЊЃКЃЈ1ЃЌ4ЃЉЛђЃЈ1ЃЌЉ2ЃЉЛђЃЈ1ЃЌ![]() ЃЉЛђЃЈ1ЃЌ
ЃЉЛђЃЈ1ЃЌ![]() ЃЉЃЛЃЈ2ЃЉ
ЃЉЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉКЏЪ§ЕФЖдГЦжсxЃНЉ![]() ЃН1ЃЌдђЕуBЃЈ3ЃЌ0ЃЉЃЌМДПЩЧѓНтЃЛ
ЃН1ЃЌдђЕуBЃЈ3ЃЌ0ЃЉЃЌМДПЩЧѓНтЃЛ
ЃЈ2ЃЉЗжPBЮЊаББпЁЂPCЮЊаББпЁЂBCЮЊаББпШ§жжЧщПіЃЌЗжБ№ЧѓНтМДПЩЃЛ
ЃЈ3ЃЉЁїMBCЕФУцЛ§SЃН![]() ЁСMNЁфЁСOBЃН
ЁСMNЁфЁСOBЃН![]() ЃЈЉx2+2x+3+xЉ3ЃЉЃН
ЃЈЉx2+2x+3+xЉ3ЃЉЃН![]() ЃЈЉx2+3xЃЉЃНЉ3x2+
ЃЈЉx2+3xЃЉЃНЉ3x2+![]() xЃЌЉ3ЃМ0ЃЌЙЪSгазюДѓжЕЮЊ
xЃЌЉ3ЃМ0ЃЌЙЪSгазюДѓжЕЮЊ![]() ЃЌДЫЪБЕуMЃЈ
ЃЌДЫЪБЕуMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛHNЁфЃН
ЃЉЃЛHNЁфЃН![]() BNЁфЃЌMN+
BNЁфЃЌMN+![]() BNзюаЁжЕЃНMNЁф+NЁфHЃНMHЃЌМДЕуNЁфЮЊЫљЧѓЕФЕуNЃЌМДПЩЧѓНтЃЎ
BNзюаЁжЕЃНMNЁф+NЁфHЃНMHЃЌМДЕуNЁфЮЊЫљЧѓЕФЕуNЃЌМДПЩЧѓНтЃЎ
ЃЈ1ЃЉКЏЪ§ЕФЖдГЦжсxЃНЉ![]() ЃН1ЃЌдђЕуBЃЈ3ЃЌ0ЃЉЃЌ
ЃН1ЃЌдђЕуBЃЈ3ЃЌ0ЃЉЃЌ
дђХзЮяЯпЕФБэДяЪНЮЊЃКyЃНЉЃЈx+1ЃЉЃЈxЉ3ЃЉЃНЉЃЈx2Љ2xЉ3ЃЉЃНЉx2+2x+3ЃЛ
ДцдкЃЌРэгЩЃК
ЩшЃКЕуPЃЈ1ЃЌmЃЉЃЌ
дђPB2ЃНm2+4ЃЌPC2ЃНЃЈmЉ3ЃЉ2+1ЃЌBC2ЃН18ЃЌ
ЂйЕБPBЮЊаББпЪБЃЌдђm2+4ЃНЃЈmЉ3ЃЉ2+1+18ЃЌНтЕУЃКmЃН4ЃЛ
ЂкЕБPCЮЊаББпЪБЃЌЭЌРэПЩЕУЃКmЃНЉ2ЃЛ
ЂлЕБBCЮЊаББпЪБЃЌЭЌРэПЩЕУЃКmЃН![]() ЃЛ
ЃЛ
ЙЪЕуPЕФзјБъЮЊЃКЃЈ1ЃЌ4ЃЉЛђЃЈ1ЃЌЉ2ЃЉЛђЃЈ1ЃЌ![]() ЃЉЛђЃЈ1ЃЌ
ЃЉЛђЃЈ1ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ2ЃЉЙ§ЕуMзїMNЁЭxжсгкЕуHЃЌНЛBCгкЕуNЁфЃЌ
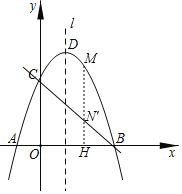
НЋЕуBЁЂCЕФзјБъДњШывЛДЮКЏЪ§БэДяЪНВЂНтЕУЃК
жБЯпBCЕФБэДяЪНЮЊЃКyЃНЉx+3ЃЌдђЁЯCBAЃН45ЁуЃЌ
ЩшЕуMЃЈxЃЌЉx2+2x+3ЃЉЃЌдђЕуNЁфЃЈxЃЌЉx+3ЃЉЃЌ
ЁїMBCЕФУцЛ§SЃН![]() ЁСMNЁфЁСOBЃН
ЁСMNЁфЁСOBЃН![]() ЃЈЉx2+2x+3+xЉ3ЃЉЃН
ЃЈЉx2+2x+3+xЉ3ЃЉЃН![]() ЃЈЉx2+3xЃЉЃНЉ3x2+
ЃЈЉx2+3xЃЉЃНЉ3x2+![]() xЃЌ
xЃЌ
ЁпЉ3ЃМ0ЃЌЙЪSгазюДѓжЕЮЊ![]() ЃЌДЫЪБЕуMЃЈ
ЃЌДЫЪБЕуMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
HNЁфЃН![]() BNЁфЃЌ
BNЁфЃЌ
MN+![]() BNзюаЁжЕЃНMNЁф+NЁфHЃНMHЃЌМДЕуNЁфЮЊЫљЧѓЕФЕуNЃЌ
BNзюаЁжЕЃНMNЁф+NЁфHЃНMHЃЌМДЕуNЁфЮЊЫљЧѓЕФЕуNЃЌ
ЙЪMN+![]() BNзюаЁжЕЮЊЃНMHЃНyMЃН
BNзюаЁжЕЮЊЃНMHЃНyMЃН![]() ЃЎ
ЃЎ


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдквЛИіВЛЭИУїЕФзРУцЩЯЃЌБГУцГЏЩЯАкЗХзХЭЌвЛЗљЦЫПЫХЦжаЕФШ§еХЦЫПЫХЦЃЌЫќУЧЗжБ№ЪЧКьЬвAЁЂЗНПщ6ЁЂКкЬв9.НЋКьЬвAЁЂЗНПщ6ЁЂКкЬв9ЩЯЪ§зжЗжБ№МЧЮЊЪ§зж1ЁЂ6ЁЂ9.НЋЫќУЧЯДдШКѓЃЌаЁКьЯШДгжаЫцЛњГщШЁвЛеХЦЫПЫХЦМЧЯТЪ§зжКѓЗХЛиЃЌЯДдШКѓЃЌдйЫцЛњГщШЁвЛеХЦЫПЫХЦМЧЯТЪ§зж.гУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓаЁУїСНДЮГщШЁЕФЦЫПЫХЦЕФЪ§зжжЎКЭЪЧ5ЕФБЖЪ§ЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
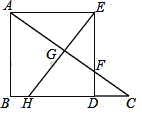
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯB=90ЁуЃЌBC>ABЃЌдкBCБпЩЯШЁЕуDЃЌЪЙAB=BDЃЌЙЙдье§ЗНаЮABDEЃЌDEНЛACгкЕуFЃЌзїEGЁЭACНЛACгкЕуGЃЌНЛBCгкЕуHЃЎ
(1)ЧѓжЄЃКЁїAEFЁеЁїEDHЃЎ
(2)ШєAB=3ЃЌDH=2DFЃЌЧѓBCЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЮЊЁбOЕФжБОЖЃЌCЮЊЁбOЩЯвЛЕуЃЌЁЯABCЕФЦНЗжЯпНЛЁбOгкЕуDЃЌDEЁЭBCгкЕуEЃЎ
ЃЈ1ЃЉЪдХаЖЯDEгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉЙ§ЕуDзїDFЁЭABгкЕуFЃЌШєBE=3![]() ЃЌDF=3ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ
ЃЌDF=3ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
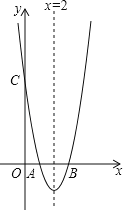
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§ЕФЭМЯѓгыxжсНЛгкЕуAЃЈ1ЃЌ0ЃЉКЭЕуBЃЌгыyжсНЛгкЕуCЃЈ0ЃЌ6ЃЉЃЌЖдГЦжсЮЊжБЯпxЃН2ЃЌЖЅЕуЮЊDЃЎЧѓЖўДЮКЏЪ§ЕФНтЮіЪНМАЫФБпаЮADBCЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
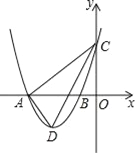
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌХзЮяЯпy=ax2+bx+3гыxжсНЛгкAЃЈЉ4ЃЌ0ЃЉЁЂBЃЈЉlЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЌЕуDЪЧЕкШ§ЯѓЯоЕФХзЮяЯпЩЯвЛЖЏЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшЕуDЕФКсзјБъЮЊmЃЌЁїACDЕФУцЛ§ЮЊСПЧѓГіSгыmЕФКЏЪ§ЙиЯЕЪНЃЌВЂШЗЖЈmЮЊКЮжЕЪБSгазюДѓжЕЃЌзюДѓжЕЪЧЖрЩйЃП
ЃЈ3ЃЉШєЕуPЪЧХзЮяЯпЖдГЦжсЩЯвЛЕуЃЌЪЧЗёДцдкЕуPЪЙЕУЁЯAPC=90ЁуЃПШєДцдкЃЌЧыжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌBдкxжсЩЯЃЌЫФБпаЮOACBЮЊЦНааЫФБпаЮЃЌЧв
ЁЯAOB=60ЁуЃЌЗДБШР§КЏЪ§![]() ЃЈkЃО0ЃЉдкЕквЛЯѓЯоФкЙ§ЕуAЃЌЧвгыBCНЛгкЕуFЁЃЕБFЮЊBCЕФжаЕуЃЌЧвSЁїAOFЃН12
ЃЈkЃО0ЃЉдкЕквЛЯѓЯоФкЙ§ЕуAЃЌЧвгыBCНЛгкЕуFЁЃЕБFЮЊBCЕФжаЕуЃЌЧвSЁїAOFЃН12![]() ЪБЃЌOAЕФГЄЮЊ____.
ЪБЃЌOAЕФГЄЮЊ____.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕуЕФзјБъЗжБ№ЮЊAЃЈЉ5ЃЌ1ЃЉЃЌBЃЈЉ2ЃЌ2ЃЉЃЌCЃЈЉ1ЃЌ4ЃЉЃЌЧыАДЯТСавЊЧѓЛЭМЃК
ЃЈ1ЃЉНЋЁїABCЯШЯђгвЦНвЦ4ИіЕЅЮЛГЄЖШЁЂдйЯђЯТЦНвЦ1ИіЕЅЮЛГЄЖШЃЌЕУЕНЁїA1B1C1ЃЌЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉЛГігыЁїABCЙигкдЕуOГЩжааФЖдГЦЕФЁїA2B2C2ЃЌВЂжБНгаДГіЕуA2ЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЪщЗЈЪЧЮвЙњЕФЮФЛЏЙхБІЃЌбаЯАЪщЗЈФмХрбјИпбХЕФЦЗИёЃЎФГаЃЮЊМгЧПЪщЗЈНЬбЇЃЌСЫНтбЇЩњЯжгаЕФЪщаДФмСІЃЌЫцЛњГщШЁСЫВПЗжбЇЩњНјааВтЪдЃЌВтЪдНсЙћЗжЮЊгХауЁЂСМКУЁЂМАИёЁЂВЛМАИёЫФИіЕШМЖЃЌЗжБ№гУAЃЌBЃЌCЃЌDБэЪОЃЌВЂНЋВтЪдНсЙћЛцжЦГЩШчЭМСНЗљВЛЭъећЕФЭГМЦЭМЃЎ
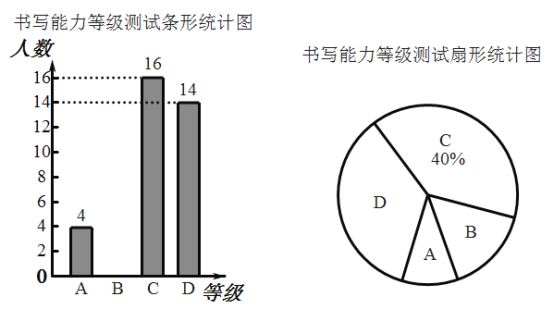
ЧыИљОнЭГМЦЭМжаЕФаХЯЂНтД№вдЯТЮЪЬтЃК
ЃЈ1ЃЉБОДЮГщШЁЕФбЇЩњШЫЪ§ЪЧ ШЫЃЌЩШаЮЭГМЦЭМжаAЫљЖдгІЩШаЮдВаФНЧЕФЖШЪ§ЪЧ ЃЎ
ЃЈ2ЃЉАбЬѕаЮЭГМЦЭМВЙГфЭъећЃЎ
ЃЈ3ЃЉШєИУбЇаЃЙВга2800ШЫЃЌЕШМЖДяЕНгХауЕФШЫЪ§ДѓдМгаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com