
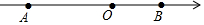 如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.
如图,数轴上有A、B两点,AB=12,原点O是线段AB上的一点,OA=2OB.分析 (1)由AO=2OB可知,将12平均分成三份,AO占两份为8,OB占一份为4,由图可知,A在原点的左边,B在原点的右边,从而得出结论;
(2)分两种情况:①点C在原点的左边,即在线段OA上时,②点C在原点的右边,即在线段OB上时,分别根据AC=CO+CB列式即可;
(3)①分两种情况:点P在原点的左侧和右侧时,OP表示的代数式不同,OQ=4+t,分别代入2OP-OQ=4列式即可求出t的值;
②点M运动的时间就是点P从点O开始到追到点Q的时间,设点M运动的时间为t秒,列式为t(2-1)=8,解出即可解决问题.
解答 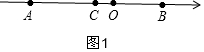 解:(1)∵AB=12,AO=2OB,
解:(1)∵AB=12,AO=2OB,
∴AO=8,OB=4,
∴A点所表示的实数为-8,B点所表示的实数为4;
(2)设C点所表示的实数为x,
分两种情况:①点C在线段OA上时,则x<0,如图1,
∵AC=CO+CB,
∴8+x=-x+4-x,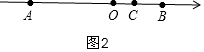
3x=-4,
x=-$\frac{4}{3}$;
②点C在线段OB上时,则x>0,如图2,
∵AC=CO+CB,
∴8+x=4,
x=-4(不符合题意,舍);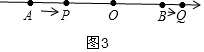
综上所述,C点所表示的实数是-$\frac{4}{3}$;
(3)①当0<t<4时,如图3,
AP=2t,OP=8-2t,BQ=t,OQ=4+t,
∵2OP-OQ=4,
∴2(8-2t)-(4+t)=4,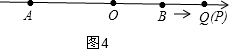
t=$\frac{8}{5}$=1.6,
当点P与点Q重合时,如图4,
2t=12+t,t=12,
当4<t<12时,如图5,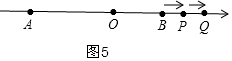
OP=2t-8,OQ=4+t,
则2(2t-8)-(4+t)=4,
t=8,
综上所述,当t为1.6秒或8秒时,2OP-OQ=4;
②当点P到达点O时,8÷2=4,此时,OQ=4+t=8,即点Q所表示的实数为8,
如图6,设点M运动的时间为t秒,
由题意得:2t-t=8,
t=8,
此时,点P表示的实数为8×2=16,所以点M表示的实数也是16,
∴点M行驶的总路程为:3×8=24,
答:点M行驶的总路程为24和点M最后位置在数轴上对应的实数为16.
点评 本题考查了数轴上两点的距离、数轴上点的表示、一元一次方程的应用,比较复杂,要认真理清题意,并注意数轴上的点,原点左边表示负数,右边表示正数,在数轴上,两点的距离等于任意两点表示的数的差的绝对值.


 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 300米 | B. | 150米 | C. | 100米 | D. | 80米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
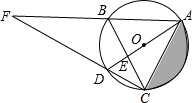 如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:
如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=60°,∠ACB=50°,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,使点A1,A2,A3在直线y=x+1上,点C1,C2,C3在x轴上,若按此规律放置正方形A2017B2017C2017C2016,则点B2017的纵坐标为22016.
将正方形A1B1C1O,A2B2C2C1,A3B3C3C2按如图所示方式放置,使点A1,A2,A3在直线y=x+1上,点C1,C2,C3在x轴上,若按此规律放置正方形A2017B2017C2017C2016,则点B2017的纵坐标为22016.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 进价(元/只) | 售价(元/只) | |
| 甲种节能灯 | 30 | 40 |
| 乙种节能灯 | 35 | 50 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com