
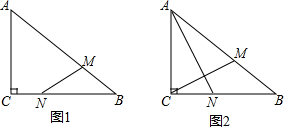
分析 (1)分两种情形当△BNM∽△BCA时,可得$\frac{BN}{BC}$=$\frac{BM}{BA}$.当△BNM∽△BAC时,可得$\frac{BN}{AB}$=$\frac{BM}{BC}$,分别列出方程求解即可;
(2)如图1中,作MH⊥BC于H.根据,S△BMN=$\frac{9}{40}$S△ABC,列出方程即可解决问题;
(3)如图2中,作MH⊥BC于H.首先证明∠MCH=∠CAN,根据tan∠CAN=tan∠MCH,列出方程即可解决问题;
解答 解:(1)在Rt△ABC中,∵∠ACB=90°,AC=6cm,BC=8cm,
∴AB=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∵CN=2t,BM=3t,
当△BNM∽△BCA时,
$\frac{BN}{BC}$=$\frac{BM}{BA}$,
∴$\frac{8-2t}{8}$=$\frac{3t}{10}$,
∴t=$\frac{20}{11}$.
当△BNM∽△BAC时,
$\frac{BN}{AB}$=$\frac{BM}{BC}$,
∴$\frac{8-2t}{10}$=$\frac{3t}{8}$,
∴t=$\frac{32}{23}$.
综上所述,t=$\frac{20}{11}$s或$\frac{32}{23}$s时,以B、M、N为顶点的三角形与△ABC相似.
(2)如图1中,作MH⊥BC于H.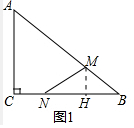
∵MH∥AC,
∴$\frac{MH}{AC}$=$\frac{BM}{BA}$,
∴$\frac{MH}{6}$=$\frac{3t}{10}$,
∴MH=$\frac{9}{5}$t,
∵S△BMN=$\frac{9}{40}$S△ABC,
∴$\frac{1}{2}$•(8-2t)•$\frac{9}{5}$t=$\frac{9}{40}$•$\frac{1}{2}$•6•8,
整理得t2-4t+3=0,
解得t=1或3.
∴当t=1s或3s时,S△BMN=$\frac{9}{40}$S△ABC.
(3)如图2中,作MH⊥BC于H.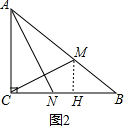
∵∠MCB+∠ACM=90°,∠CAN+∠ACM=90°,
∴∠MCH=∠CAN,
∴tan∠CAN=tan∠MCH,
∴$\frac{2t}{6}$=$\frac{\frac{9}{5}t}{8-\frac{12}{5}t}$,
解得t=$\frac{40}{39}$,
∴t=$\frac{40}{39}$s时,AN⊥CM.
点评 本题考查相似形综合题、锐角三角函数、平行线分线段成比例定理、勾股定理等知识,解题的关键是学会添加常用辅助线,学会用分类讨论的首先思考问题,学会利用参数构建方程解决问题,属于中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD的边长为6$\sqrt{2}$,点E是边CD的中点,点F在边BC上,AE、AF分别与对角线BD交于点G、H,点M、N分别是线段GH、EF的中点,若∠EAF=45°,则线段MN的长为$\frac{5}{2}$.
如图,正方形ABCD的边长为6$\sqrt{2}$,点E是边CD的中点,点F在边BC上,AE、AF分别与对角线BD交于点G、H,点M、N分别是线段GH、EF的中点,若∠EAF=45°,则线段MN的长为$\frac{5}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
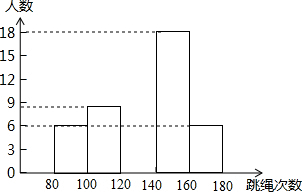 为了了解我县八年级学生的身体素质情况,随机抽取了50名学生进行一分钟跳绳次数测试,将测试情况绘制出部分频数分布表和部分频数分布直方图如图.
为了了解我县八年级学生的身体素质情况,随机抽取了50名学生进行一分钟跳绳次数测试,将测试情况绘制出部分频数分布表和部分频数分布直方图如图.| 组别 | 次数x | 频数(人数) |
| 第1组 | 80≤x<100 | 6 |
| 第2组 | 100≤x<120 | 8 |
| 第3组 | 120≤x<140 | a |
| 第4组 | 140≤x<160 | 18 |
| 第5组 | 160≤x<180 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com