【题目】已知A（3，y1）、B（4，y2）都在抛物线y=x2+1上，试比较y1与y2的大小：__________．
科目：初中数学 来源： 题型：
【题目】下列四个命题中，真命题的是( )
A. 相等的圆心角所对的弧相等 B. 同旁内角互补
C. 平行四边形是轴对称图形 D. 全等三角形对应边上的高相等
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料：
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗？
小敏在思考问题时，有如下思路：连接AC．
结合小敏的思路作答：
（1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决一下问题；
（2）如图2，在（1）的条件下，若连接AC，BD．
①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论．
查看答案和解析>>
科目：初中数学 来源： 题型：
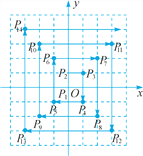
【题目】如图，在平面直角坐标系中，每个最小方格的边长均为1个单位，P1，P2，P3，…均在格点上，其顺序按图中“→”方向排列，如：点P1(0，0)，P2(0，1)，P3(1，1)，P4(1，－1)，P5(－1，－1)，P6(－1，2)，….根据这个规律，求点P2018的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图①，直线y=
x+4交于x轴于点A，交y轴于点C，过A、C两点的抛物线F1交x轴于另一点B（1，0）．
（1）求抛物线F1所表示的二次函数的表达式；
（2）若点M是抛物线F1位于第二象限图象上的一点，设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC，记S=S四边形MAOC﹣S△BOC，求S最大时点M的坐标及S的最大值；
（3）如图②，将抛物线F1沿y轴翻折并“复制”得到抛物线F2，点A、B与（2）中所求的点M的对应点分别为A′、B′、M′，过点M′作M′E⊥x轴于点E，交直线A′C于点D，在x轴上是否存在点P，使得以A′、D、P为顶点的三角形与△AB′C相似？若存在，请求出点P的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
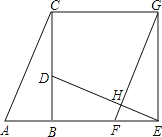
【题目】如图，已知Rt△ABC中，∠ABC=90°，先把△ABC绕点B顺时针旋转90°至△DBE后，再把△ABC沿射线AB平移至△FEG，DE、FG相交于点H．
（1）判断线段DE、FG的位置关系，并说明理由；
（2）连结CG，求证：四边形CBEG是正方形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】下列调查中必须用抽样调查方式来收集数据的有（ ）
①检查一大批灯泡使用寿命的长短.②调查某大城市居民家庭的收入情况.
③了解全班同学的身高情况.④检查某种药品的药数.
A. 1个 B. 2个 c. 3个 C. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
