
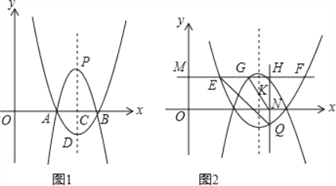
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.
【答案】(1)(3,﹣1)(2)①二次函数y2=ax2+bx+c(a≠0)的图象过点B②(3﹣![]() ,1)、(3+
,1)、(3+![]() ,1)或(3,﹣1)③当△GHN∽△EHQ,实数m的值为1.
,1)或(3,﹣1)③当△GHN∽△EHQ,实数m的值为1.
【解析】(1)∵y1=(x﹣2)(x﹣4)=x2﹣6x+8=(x﹣3)2﹣1,
∴顶点D的坐标为(3,﹣1).故答案为:(3,﹣1).
(2)①∵点P在对称轴l上,位于点C上方,且CP=2CD,∴点P的坐标为(3,2),
∴二次函数y1=(x﹣2)(x﹣4)与y2=ax2+bx+c的图象的对称轴均为x=3,
∵点A、B关于直线x=3对称,∴二次函数y2=ax2+bx+c(a≠0)的图象过点B.
②∵二次函数y2=ax2+bx+c的顶点坐标P(3,2),且图象上有且只有三个点到x轴的距离等于2d,∴2d=2,解得:d=1.令y1=(x﹣2)(x﹣4)=x2﹣6x+8中y1=±1,即x2﹣6x+8=±1,
解得:x1=3﹣![]() ,x2=3+
,x2=3+![]() ,x3=3,∴点R的坐标为(3﹣
,x3=3,∴点R的坐标为(3﹣![]() ,1)、(3+
,1)、(3+![]() ,1)或(3,﹣1).
,1)或(3,﹣1).
故答案为:(3﹣![]() ,1)、(3+
,1)、(3+![]() ,1)或(3,﹣1).
,1)或(3,﹣1).
③设过点M平行x轴的直线交对称轴l于点K,直线l也是二次函数y2=ax2+bx+c(a≠0)的图象的对称轴.
∵二次函数y2=ax2+bx+c过点A、B,且顶点坐标为P(3,2),
∴二次函数y2=﹣2(x﹣2)(x﹣4).
设N(n,0),则H(n,﹣2(n﹣2)(n﹣4)),Q(n,(n﹣2)(n﹣4)),
∴HN=2(n﹣2)(n﹣4),QN=(n﹣2)(n﹣4),∴![]() =2,即
=2,即![]() =
=![]() .
.
∵△GHN∽△EHQ,∴![]() .∵G、H关于直线l对称,∴KG=KH=
.∵G、H关于直线l对称,∴KG=KH=![]() HG,∴
HG,∴![]() .
.
设KG=t(t>0),则G的坐标为(3﹣t,m),E的坐标为(3﹣2t,m),
由题意得:![]() ,解得:
,解得: 或
或![]() (舍去).
(舍去).
故当△GHN∽△EHQ,实数m的值为1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)已知4m=a,8n=b,用含a,b的式子表示下列代数式: ①求:22m+3n的值,
②求:24m﹣6n的值;
(2)已知2×8x×16=223,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年春季我国西南五省持续干旱,旱情牵动着全国人民的心.“一方有难、八方支援”,某厂计划生产1 800吨纯净水支援灾区人民,为尽快把纯净水发往灾区,工人把每天的工作效率提高到原计划的1.5倍,结果比原计划提前3天完成了生产任务.求原计划每天生产多少吨纯净水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“唱红歌”歌唱比赛,九年级(1)班、九年级(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
(1)九(1)班复赛成绩的中位数是九(2)班复赛成绩的众数是 .
(2)计算九(1)班复赛成绩的平均数和方差.
(3)已知九(2)班复赛成绩的方差是160,则复赛成绩较为稳定的是班.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com