
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,与x轴交于另一点B.
两点,与x轴交于另一点B.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
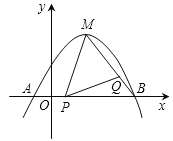
![]() 若抛物线的顶点为M,点P为线段OB上一动点
若抛物线的顶点为M,点P为线段OB上一动点![]() 不与点B重合
不与点B重合![]() ,点Q在线段MB上移动,且
,点Q在线段MB上移动,且![]() ,设线段
,设线段![]() ,
,![]() ,求
,求![]() 与x的函数关系式,并直接写出自变量x的取值范围;
与x的函数关系式,并直接写出自变量x的取值范围;
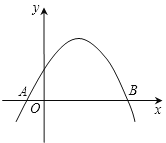
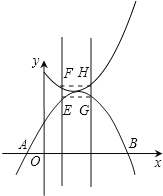
![]() 在同一平面直角坐标系中,两条直线
在同一平面直角坐标系中,两条直线![]() ,
,![]() 分别与抛物线交于点E、G,与
分别与抛物线交于点E、G,与![]() 中的函数图象交于点F、
中的函数图象交于点F、![]() 问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
问四边形EFHG能否成为平行四边形?若能,求m、n之间的数量关系;若不能,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)m、n之间的数量关系是
;(3)m、n之间的数量关系是![]() 且
且![]() .
.
【解析】
![]() 将A、C的坐标代入抛物线的解析式中,即可求出
将A、C的坐标代入抛物线的解析式中,即可求出![]() 的函数解析式;
的函数解析式;
![]() 过M作
过M作![]() 轴于N,根据抛物线
轴于N,根据抛物线![]() 的函数解析式,即可得到M点的坐标,可分别在
的函数解析式,即可得到M点的坐标,可分别在![]() 和
和![]() 中,用勾股定理表示出MN的长,由此可得到关于PM、x的函数关系式;由于
中,用勾股定理表示出MN的长,由此可得到关于PM、x的函数关系式;由于![]() ,易证得
,易证得![]() ∽
∽![]() ,根据相似三角形得到的比例线段即可得到关于PM、
,根据相似三角形得到的比例线段即可得到关于PM、![]() 的关系式,联立两式即可求出
的关系式,联立两式即可求出![]() 、x的函数关系式;
、x的函数关系式;
![]() 根据两根抛物线的解析式和两条直线的解析式,可求出E、F、G、H四点的坐标,即可得到EF、GH的长,由于
根据两根抛物线的解析式和两条直线的解析式,可求出E、F、G、H四点的坐标,即可得到EF、GH的长,由于![]() ,若四边形EFHG是平行四边形,那么必有
,若四边形EFHG是平行四边形,那么必有![]() ,可据此求出m、n的数量关系.
,可据此求出m、n的数量关系.
解:![]() 抛物线
抛物线![]() 经过
经过![]() ,
,![]() 两点;
两点;
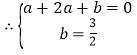 ,
,
解得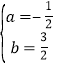 .
.
![]() 抛物线的解析式为
抛物线的解析式为![]() ;
;
![]() 作
作![]() ,垂足为N.
,垂足为N.
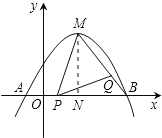
由![]() ,易得
,易得![]() ,
,![]() ,
,![]() ,
,![]() ;
;
![]() ,
,![]() ,
,![]() ,
,![]() ;
;
根据勾股定理有:![]() ,
,
![]() ;
;
又![]() ,
,![]() 公共角
公共角![]() ,
,
![]() ∽
∽![]() ,
,
![]() ;
;
由![]() 得:
得:![]() ;
;
![]() ,
,
![]() 与x的函数关系式为
与x的函数关系式为![]() ;
;
![]() 四边形EFHG可以为平行四边形,m、n之间的数量关系是:
四边形EFHG可以为平行四边形,m、n之间的数量关系是:![]() 且
且![]() ;
;
![]() 点E、G是抛物线
点E、G是抛物线![]() 分别与直线
分别与直线![]() ,
,![]() 的交点,
的交点,
![]() 点E、G坐标为
点E、G坐标为![]() ,
,![]() ;
;
同理,点F、H坐标为![]() ,
,![]()
![]() ,
,![]() ;
;
![]() 四边形EFHG是平行四边形,
四边形EFHG是平行四边形,![]() ,
,
![]() ,
,
![]() ;
;
![]() 由题意知
由题意知![]() ,
,
![]() ;
;
因此四边形EFHG可以为平行四边形,m、n之间的数量关系是![]() 且
且![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:如图,在矩形ABCD中,M、N分别是边AD、BC的中点,E、F分别是线段BM、CM的中点
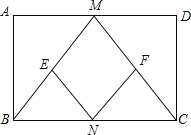
(1)求证:△ABM≌△DCM
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB= _时,四边形MENF是正方形(只写结论,不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,D是AC边上的一个动点,将
,D是AC边上的一个动点,将![]() 沿BD所在直线折叠,使点A落在点E处.
沿BD所在直线折叠,使点A落在点E处.
![]() 如图
如图![]() ,若点D是AC的中点,连接
,若点D是AC的中点,连接![]() 求证:四边形BCED是平行四边形;
求证:四边形BCED是平行四边形;
![]() 如图
如图![]() ,若
,若![]() ,求
,求![]() 的值.
的值.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小烨在探究数轴上两点间距离时发现:若![]() 两点在
两点在![]() 轴上或与
轴上或与![]() 轴平行,
轴平行,![]() 两点的横坐标分别为
两点的横坐标分别为![]() ,则
,则![]() 两点间距离为
两点间距离为![]() ;若
;若![]() 两点在
两点在![]() 轴上或与
轴上或与![]() 轴平行,
轴平行,![]() 两点的纵坐标分别为
两点的纵坐标分别为![]() ,则
,则![]() 两点间距离为
两点间距离为![]() .据此,小烨猜想:对于平面内任意两点
.据此,小烨猜想:对于平面内任意两点![]() ,
,![]() 两点间的距离为
两点间的距离为![]() .
.
(1)请你利用下图,试证明:;
(2)若![]() ,试在
,试在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 的距离最短,并求出
的距离最短,并求出![]() 的最小值和
的最小值和![]() 点坐标.
点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王抽样调查了本地若干天的空气质量情况,把空气质量分成四类:![]() 类,
类,![]() 类,
类,![]() 类和
类和![]() 类,分别对应的质量级别为优、良、轻度污染和中度污染四种情况,并绘制两个统计图(部分信息缺失);
类,分别对应的质量级别为优、良、轻度污染和中度污染四种情况,并绘制两个统计图(部分信息缺失);
空气质量条形统计图
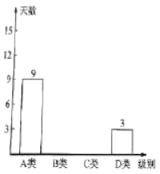
空气质量扇形统计图
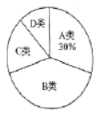
(1)本次调查的样本容量是________;
(2)已知![]() 类和
类和![]() 类在扇形统计图中所占的夹角为
类在扇形统计图中所占的夹角为![]() 度,
度,![]() 类的频数是
类的频数是![]() 类的
类的![]() 倍,通过计算,求出
倍,通过计算,求出![]() 类和
类和![]() 类的频数,并完成条形统计图;
类的频数,并完成条形统计图;
(3)计算![]() 类在扇形统计图中所对应的圆心角度数;
类在扇形统计图中所对应的圆心角度数;
(4)若一年按![]() 天计算,求本地全年空气质量达到优良以上的天数(保留整数).
天计算,求本地全年空气质量达到优良以上的天数(保留整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队用甲、乙两台隧道挖掘机从两个方向挖掘同一条隧道,因为地质条件不同,甲、乙的挖掘速度不同,已知甲、乙同时挖掘![]() 天,可以挖
天,可以挖![]() 米,若甲挖
米,若甲挖![]() 天,乙挖
天,乙挖![]() 天可以挖掘
天可以挖掘![]() 米.
米.
(1)请问甲、乙挖掘机每天可以挖掘多少米?
(2)若乙挖掘机比甲挖掘每小时多挖掘![]() 米,甲、乙每天挖掘的时间相同,求甲每小时挖掘多少米?
米,甲、乙每天挖掘的时间相同,求甲每小时挖掘多少米?
(3)若隧道的总长为![]() 米,甲、乙挖掘机工作
米,甲、乙挖掘机工作![]() 天后,因为甲挖掘机进行设备更新,乙挖掘机设备老化,甲比原来每天多挖
天后,因为甲挖掘机进行设备更新,乙挖掘机设备老化,甲比原来每天多挖![]() 米,同时乙比原来少挖
米,同时乙比原来少挖![]() 米
米![]() .最终,甲、乙两台挖掘机在相同时间里各完成隧道总长的一半,请用含
.最终,甲、乙两台挖掘机在相同时间里各完成隧道总长的一半,请用含![]() ,
,![]() 的代数式表示
的代数式表示![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
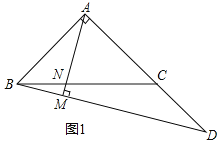
【题目】如图,在![]() 中,
中,![]() ,点D为AC延长线上一点,连接BD,过A作
,点D为AC延长线上一点,连接BD,过A作![]() ,垂足为M,交BC于点N
,垂足为M,交BC于点N
![]() 如图1,若
如图1,若![]() ,
,![]() ,求AM的长;
,求AM的长;
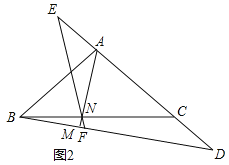
![]() 如图2,点E在CA的延长线上,且
如图2,点E在CA的延长线上,且![]() ,连接EN并延长交BD于点F,求证:
,连接EN并延长交BD于点F,求证:![]() ;
;
![]() 在
在![]() 的条件下,当
的条件下,当![]() 时,请求出
时,请求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,在等腰
,在等腰![]() 中,
中,![]() ,点E在AC上
,点E在AC上![]() 且不与点A、C重合
且不与点A、C重合![]() ,在
,在![]() 的外部作等腰
的外部作等腰![]() ,使
,使![]() ,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
![]() 请直接写出线段AF,AE的数量关系;
请直接写出线段AF,AE的数量关系;
![]() 将
将![]() 绕点C逆时针旋转,当点E在线段BC上时,如图
绕点C逆时针旋转,当点E在线段BC上时,如图![]() ,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
,连接AE,请判断线段AF,AE的数量关系,并证明你的结论;
![]() 若
若![]() ,
,![]() ,在图
,在图![]() 的基础上将
的基础上将![]() 绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.
绕点C继续逆时针旋转一周的过程中,当平行四边形ABFD为菱形时,直接写出线段AE的长度.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com