
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ] = ;[
] = ;[![]() ] = .
] = .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.
]=1,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有A,B两种商品,买2件A商品和1件B商品用了90元,买3件A商品和2件B商品共用了160元.
(1)求A,B两种商品每件多少元?
(2)如果小亮准备购买A,B两种商品共10件,总费用不超过350元,且不低于300元,问有几种购买方案,哪种方案费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从①∠1=∠2;②∠C=∠D;③∠A=∠F三个条件中选出两个作为已知条件,另一个作为结论所组成的命题中,正确命题的个数为( )

A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,E,F是对角线BD上的两点,如果添加一个条件,使△ABE≌△CDF,则添加的条件不能为( )
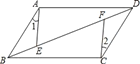
A. BE=DF B. BF=DE C. AE=CF D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)求证:四边形AECF是平行四边形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,某学习小组对有一内角(∠BAD)为120°的平行四边形ABCD,将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
(3)深入探究:在(2)的条件下,学习小组某成员探究发现AE+2AF= ![]() AC,试判断结论是否正确,并说明理由.
AC,试判断结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
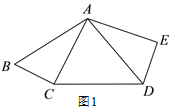
【题目】如图 1,在五边形 ABCDE 中,∠E=90°,BC=DE.连接 AC,AD, 且 AB=AD,AC⊥BC.
(1)求证:AC=AE;
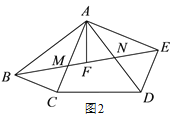
(2)如图 2,若∠ABC=∠CAD,AF 为 BE 边上的中线,求证:AF⊥CD;
(3)如图 3,在(2)的条件下,AE=6,DE=4,则五边形 ABCDE 的面积为_____.
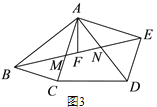
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com