(2010•乌鲁木齐)已知二次函数y=ax2+bx+c(a≠0)的图象经过O(0,0),M(1,1)和N(n,0)
(n≠0)三点.
(1)若该函数图象顶点恰为M点,写出此时n的值及y的最大值;
(2)当n=-2时,确定这个二次函数的解析式,并判断此时y是否有最大值;
(3)由(1)、(2)可知,n的取值变化,会影响该函数图象的开口方向.请求出n满足什么条件时,y有最小值.
【答案】
分析:(1)M点为顶点,则O、N关于x=1对称,M点为最大值点,由此得出答案;
(2)由于抛物线的图象经过原点,故c=0;将M、N两点坐标代入y=ax
2+bx联立求解,并由解出的a值判断是否有最大值;
(3)将M、N两点坐标代入y=ax
2+bx联立得出含a、n的方程,由a>0确定n满足的条件.
解答:解:(1)由二次函数图象的对称性可知n=2;
y的最大值为1.
(2)由题意得:
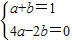
,
解这个方程组得:
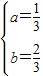
;
故这个二次函数的解析式为y=
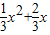
;
∵

>0,
∴y没有最大值;
(3)由题意得:
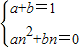
,
整理得:an
2+(1-a)n=0,即n(an+1-a)=0;(8分)
∵n≠0,
∴an+1-a=0;
故(1-n)a=1,而n≠1;
若y有最小值,则需a>0,∴1-n>0,即n<1;
∴n<1且n≠0时,y有最小值.
点评:此题主要考查了抛物线的性质、二次函数图象与系数的关系等重要知识点,难度适中.

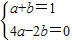 ,
,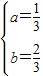 ;
;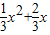 ;
; >0,
>0,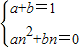 ,
,

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案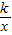 (k<0)的图象上,则y1,y2,y3的大小关系为 (用“>”或“<”连接).
(k<0)的图象上,则y1,y2,y3的大小关系为 (用“>”或“<”连接).