
分析 (1)令二次函数解析式中y=0,得到关于x的一元二次方程,求出方程的解可得出二次函数与x轴的交点坐标;
(2)将二次函数y=x2-2x-8化为顶点形式,然后比较y=x2与y=(x-1)2-9,根据图象的平移规律“上加下减、左加右减”,可得出平移的过程.
解答 解:(1)二次函数的解析式y=x2-2x-8,
令y=0,得到x2-2x-8=0,
解得:x1=4,x2=-2;
则此二次函数的图象与x轴的交点坐标分别为(-2,0)、(4,0);
(2)将二次函数y=x2-2x-8化为顶点式为y=(x-1)2-9,
∴将y=x2的图象先向右平移1个单位,再向下平移9个单位,可得到二次函数y=x2-2x-8的图象.
点评 此题考查了抛物线与x轴的交点,以及二次函数图象与几何变换,要求二次函数与x轴的交点,即要y=0,得到关于x的方程来求解;要求二次函数与y轴的交点,即要x=0,求出y的值即可,此外熟练掌握二次函数图象的平移规律是解本题第二问的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月阅读册数(本) | 1 | 2 | 3 | 4 | 5 |
| 被调查的学生数(人) | 20 | 50 | 15 | 10 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
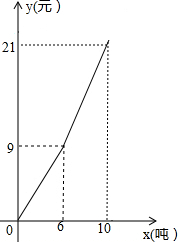 随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:
随着地球上的水资源日益枯竭,各级政府越来越重视倡导节约用水.某市市民生活用水按“阶梯水价”方式进行收费,人均月生活用水收费标准如图所示,图中x表示人均月生活用水的吨数,y表示收取的人均月生活用水费(元).请根据图象信息,回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
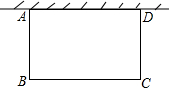 如图,某居民小区要在一块一边靠墙(墙长15m)的高地上修建一个矩形花园ABCD,花园的一边靠墙,另外三边用总长为40m的栅栏围成.则BC=15米时,花园的面积最大,最大面积是187.5平方米.
如图,某居民小区要在一块一边靠墙(墙长15m)的高地上修建一个矩形花园ABCD,花园的一边靠墙,另外三边用总长为40m的栅栏围成.则BC=15米时,花园的面积最大,最大面积是187.5平方米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com