
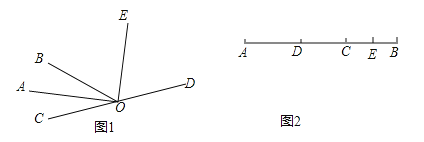
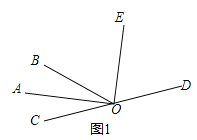
【题目】(1)如图1,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,求∠BOE,∠COE的度数.
(2)如图2,已知AB=16cm,C是AB上一点,点D是线段AC的中点,点E是线段BC的中点,求线段DE的长度.
【答案】(1)125°;(2)8cm.
【解析】试题分析:(1)已知OA平分∠BOC,∠AOC=70°,根据角平分线的定义可得∠BOD=110°,再由OE平分∠BOD,可得∠BOE=55°,根据∠COE=∠BOC+∠BOE即可求得∠COE的度数;(2)已知点D是线段AC的中点,点E是线段BC的中点,根据线段中点的定义可得DC=![]() AC,CE=
AC,CE=![]() CB,根据DE=DC+CE=
CB,根据DE=DC+CE=![]() (AC+CB)即可求得DE的长度.
(AC+CB)即可求得DE的长度.
试题解析:
(1)∵OA平分∠BOC,
∴∠BOC=2∠AOC=70°,
∴∠BOD=110°,
∵OE平分∠BOD,
∴∠BOE=55°,
∴∠COE=∠BOC+∠BOE=125°;
(2)∵点D是线段AC的中点,点E是线段BC的中点,
∴DC=![]() AC,CE=
AC,CE=![]() CB,
CB,
∴DE=DC+CE=![]() (AC+CB)=8cm.
(AC+CB)=8cm.
![]()


 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】已知∠AOB=120°,OC在它的内部,且把∠AOB分成1:3的两个角,那么∠AOC的度数为( )
A.40°
B.40°或80°
C.30°
D.30°或90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
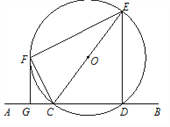
(1)求证:直线FG是⊙O的切线;
(2)若FG=4,⊙O的半径为5,求四边形FGDE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在道路改造过程中,需要铺设一条长为1000米的管道,决定由甲、乙两个工程队来完成这一工程.已知甲工程队比乙工程队每天能多铺设20米,且甲工程队铺设350米所用的天数与乙工程队铺设250米所用的天数相同.
(1)甲、乙工程队每天各能铺设多少米?
(2)如果要求完成该项工程的工期不超过10天,那么为两工程队分配工程量的方案有几种?请你帮助设计出来(工程队分配工程量为正整百数).
查看答案和解析>>
科目:初中数学 来源: 题型:
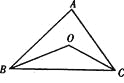
【题目】如图,在△ ABC中,∠ ABC、∠ ACB的平分线交于点O。
(1)若∠ABC=40°,∠ ACB=50°,则∠BOC=_______
(2)若∠ABC+∠ ACB=lO0°,则∠BOC="________"
(3)若∠A=70°,则∠BOC=_________
(4)若∠BOC=140°,则∠A=________
(5)你能发现∠ BOC与∠ A之间有什么数量关系吗?写出并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾的分类情况(如下图),进行整理后,绘制了如下两幅尚不完整的统计图:
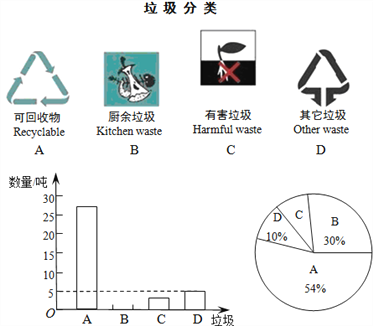
根据图表解答下列问题:
(1)请将条形统计图补充完整;
(2)在扇形统计图中,求出“D”部分所对应的圆心角等于 度;
(3)在抽样数据中,产生的有害垃圾共有 吨;
(4)调查发现,在可回收物中废纸垃圾约占![]() ,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
,若每回收1吨废纸可再造纸0.85吨.假设该城市每月产生的生活垃圾为10000吨,且全部分类处理,那么每月回收的废纸可再造纸多少吨?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( ) 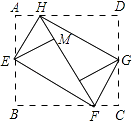
A.12cm
B.16cm
C.20cm
D.28cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF 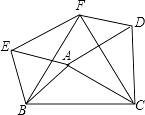
(1)求证:△EBF≌△DFC;
(2)求证:四边形AEFD是平行四边形;
(3)①△ABC满足时,四边形AEFD是菱形.(无需证明) ②△ABC满足时,四边形AEFD是矩形.(无需证明)
③△ABC满足时,四边形AEFD是正方形.(无需证明)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com