在平面内画了若干个点,任意三点都不在同一直线上,连接任意两点共得到直线45条.
(1)问该平面上共画了多少个点?
(2)解决该问题是否得到了一个一元二次方程?如果不是,指出得到的方程的名称;如果是,求出这个方程的两根之和、两根之积,并求出两根的倒数和.
解:(1)设平面内有n个点,一共可以画(n-1)+…+4+3+2+1=

=45,
整理得:n
2-n-90=0
解得:n
1=10或n
2=-9(舍去),
答:该平面上共画了10个点;
(2)问题中得到了方程:n
2-n-90=0
是有关n的一元二次方程,两根之和为1,两根之积为-90,

=

=-
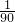
;
分析:(1)根据过两点的直线有1条,过不在同一直线上的三点的直线有3条,过任何三点都不在一条直线上四点的直线有6条,按此规律,由特殊到一般,总结出公式:平面内任意三个点都不在同一直线上,平面内有n个点,一共可以画直线的条数为

;
(2)根据上题得到的方程进行判定即可.
点评:本题考查了一元二次方程的应用,解题的关键是总结出平面内n个点连接任意两点得到的直线的条数.

 =45,
=45, =
= =-
=-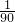 ;
; ;
;
