
【题目】已知二次函数y=ax2+bx+c(a>0)的图象的对称轴为直线x=1,且(x1,y1),(x2,y2)为其图象上的两点,( )
A. 若x1>x2>1,则(y1-y2)+2a(x1-x2)<0
B. 若1>x1>x2,则(y1-y2)+2a(x1-x2)<0
C. 若x1>x2>1,则(y1-y2)+a(x1-x2)>0
D. 若1>x1>x2,则(y1-y2)+a(x1-x2)>0
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】高中招生指标到校是我市中考招生制度改革的一项重要措施.某初级中学对该校近四年指标到校保送生人数进行了统计,制成了如下两幅不完整的统计图:
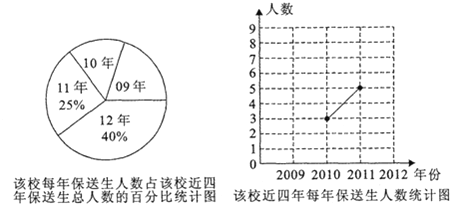
(1)该校近四年保送生人数的极差是 .请将折线统计图补充完整;
(2)该校2009年指标到校保送生中只有1位女同学,学校打算从中随机选出2位同学了解他们进人高中阶段的学习情况.请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下面两个定理:
①线段垂直平分线上的点到这条线段两个端点的距离相等;
②到一条线段两个端点距离相等的点在这条线段的垂直平分线上.
应用上述定理进行如下推理:
如图,直线l是线段MN的垂直平分线.

∵点A在直线l上,∴AM=AN.( )
∵BM=BN,∴点B在直线l上.( )
∵CM≠CN,∴点C不在直线l上.
这是∵如果点C在直线l上,那么CM=CN, ( )
这与条件CM≠CN矛盾.
以上推理中各括号内应注明的理由依次是 ( )
A. ②①① B. ②①②
C. ①②② D. ①②①
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC与△A1B1C1是位似图形.在网格上建立平面直角坐标系,使得点A的坐标为(1,﹣6).
(1)在图上标出点,△ABC与△A1B1C1的位似中心P.并写出点P的坐标为 ;
(2)以点A为位似中心,在网格图中作△AB2C2,使△AB2C2和△ABC位似,且位似比为1:2,并写出点C2的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4件同型号的产品中,有1件不合格品和3件合格品.
(1)从这4件产品中随机抽取1件进行检测,求抽到的是不合格品的概率;
(2)从这4件产品中随机抽取2件进行检测,求抽到的都是合格品的概率;
(3)在这4件产品中加入x件合格品后,进行如下试验:随机抽取1件进行检测,然后放回,多次重复这个试验,通过大量重复试验后发现,抽到合格品的频率稳定在0.95,则可以推算出x的值大约是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
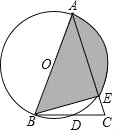
【题目】如图,在△ABC中,AB=AC,E在AC上,经过A,B,E三点的圆O交BC于点D,且D点是弧BE的中点,
(1)求证AB是圆的直径;
(2)若AB=8,∠C=60°,求阴影部分的面积;
(3)当∠A为锐角时,试说明∠A与∠CBE的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,我们把依次连接任意四边形ABCD各边中点所得四边形EFGH叫中点四边形.若四边形ABCD的面积记为S1,中点四边形EFGH的面积记为S2,则S1与S2的数量关系是( )
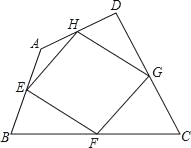
A. S1=3S2 B. 2S1=3S2 C. S1=2S2 D. 3S1=4S2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,二次函数的抛物线的顶点坐标C,与x轴的交于A(1,0)、B(﹣3,0)两点,与y轴交于点D(0,3).
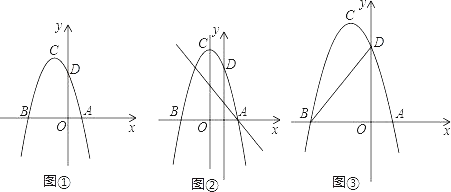
(1)求这个抛物线的解析式;
(2)如图②,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为﹣2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G、H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;
(3)如图③,连接AC交y轴于M,在x轴上是否存在点P,使以P、C、M为顶点的三角形与△AOM相似?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com