
ЁОЬтФПЁПдФЖСРэНтЃК
дВЪЧзюЭъУРЕФЭМаЮЃЌЫќОпгавЛаЉЬиЪтЕФаджЪЃКЭЌЛЁЛђЕШЛЁЫљЖдЕФдВжмНЧЯрЕШЃЌвЛЬѕЛЁЫљЖдЕФдВжмНЧЕШгкетЬѕЛЁЫљЖдЕФдВаФНЧЕФвЛАыЁЁЃЛЯШЙЙдьЁАИЈжњдВЁБЃЌдйРћгУдВЕФаджЪНЋЮЪЬтНјаазЊЛЏЃЌЭљЭљФмЛЏвўЮЊЯдЁЂЛЏФбЮЊвзЃЎ

НтОіЮЪЬтЃК
ШчЭМЃЌЕу![]() гыЕу
гыЕу![]() ЕФзјБъЗжБ№ЪЧ
ЕФзјБъЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЪЧИУжБНЧзјБъЯЕФкЕФвЛИіЖЏЕуЃЎ
ЪЧИУжБНЧзјБъЯЕФкЕФвЛИіЖЏЕуЃЎ
ЃЈ1ЃЉЪЙ![]() ЕФЕу
ЕФЕу![]() га_________ИіЃЛ
га_________ИіЃЛ
ЃЈ2ЃЉШєЕу![]() дк
дк![]() ЕФИКАыжсЩЯЃЌЧв
ЕФИКАыжсЩЯЃЌЧв![]() ЃЌЧѓТњзуЬѕМўЕФЕу
ЃЌЧѓТњзуЬѕМўЕФЕу![]() ЕФзјБъЃЛ
ЕФзјБъЃЛ
ЃЈ3ЃЉЕБ![]() ЮЊШёНЧЪБЃЌЩш
ЮЊШёНЧЪБЃЌЩш![]() ЃЌШєЕу
ЃЌШєЕу![]() дк
дк![]() жсЩЯвЦЖЏЪБЃЌТњзуЬѕМўЕФЕу
жсЩЯвЦЖЏЪБЃЌТњзуЬѕМўЕФЕу![]() га4ИіЃЌЧѓ
га4ИіЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁПЃЈ1ЃЉЮоЪ§ЃЛЃЈ2ЃЉ![]() Лђ
Лђ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЎ
ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉвдABЮЊБпзїГіЕШБпЁїABEКЭЁїABFЃЌЗжБ№вдЕуEЁЂFЮЊдВаФЃЌABЮЊАыОЖзїЁбEЁЂЁбFЃЌИљОндВжмНЧЖЈРэПЩжЊЃЌЪЙ![]() ЕФЕу
ЕФЕу![]() гаЮоЪ§ИіЃЛ
гаЮоЪ§ИіЃЛ
ЃЈ2ЃЉЙ§ЕуEзїEHЁЭyжсЃЌEGЁЭxжсЃЌДЙзуЗжБ№ЮЊHЁЂGЃЌСЌНгEC1ЃЌРћгУДЙОЖЖЈРэЧѓЕУAHЃНBHЃН3ЃЌдйИљОнОиаЮаджЪЕУEGЃНOHЃН5ЃЌOGЃНEHЃЌзюКѓРћгУЙДЙЩЖЈРэМЦЫуМДПЩЃЛ
ЃЈ3ЃЉИљОнТњзуЬѕМўЕФЕу![]() га4ИіПЩжЊЁбEЁЂЁбFгыxжсЯрНЛЃЌЕБЁбEгыxжсЯрЧагкЕуCЪБЃЌПЩЕУEBЃНECЃНOHЃН5ЃЌРћгУШ§НЧКЏЪ§ПЩЧѓЕУsinЁЯBEHЕФжЕЃЌдйИљОнДЙОЖЖЈРэМАдВжмНЧЖЈРэПЩЕУЁЯBEHЃНЁЯACBЃЌНјЖјПЩЧѓЕУЗћКЯЬтвтЕФ
га4ИіПЩжЊЁбEЁЂЁбFгыxжсЯрНЛЃЌЕБЁбEгыxжсЯрЧагкЕуCЪБЃЌПЩЕУEBЃНECЃНOHЃН5ЃЌРћгУШ§НЧКЏЪ§ПЩЧѓЕУsinЁЯBEHЕФжЕЃЌдйИљОнДЙОЖЖЈРэМАдВжмНЧЖЈРэПЩЕУЁЯBEHЃНЁЯACBЃЌНјЖјПЩЧѓЕУЗћКЯЬтвтЕФ![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
НтЃКЃЈ1ЃЉШчЭМЃЌЁїABEКЭЁїABFЮЊЕШБпШ§НЧаЮЃЌЗжБ№вдЕуEЁЂFЮЊдВаФЃЌABЮЊАыОЖзїЁбEЁЂЁбFЃЌИљОндВжмНЧЖЈРэПЩжЊЃЌЯвABЫљЖдЕФгХЛЁЩЯЕФШЮвтвЛЕуCЖМЪЙ![]() ЃЌ
ЃЌ
ЁрЪЙ![]() ЕФЕу
ЕФЕу![]() гаЮоЪ§ИіЃЛ
гаЮоЪ§ИіЃЛ
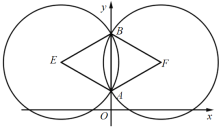
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуEзїEHЁЭyжсЃЌEGЁЭxжсЃЌДЙзуЗжБ№ЮЊHЁЂGЃЌСЌНгEC1ЃЌ

ЁпЕу![]() гыЕу
гыЕу![]() ЕФзјБъЗжБ№ЪЧ
ЕФзјБъЗжБ№ЪЧ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрOAЃН2ЃЌOBЃН8ЃЌABЃН6ЃЌ
ЁпEHЁЭyжсЃЌ
ЁрAHЃНBHЃН3ЃЌ
ЁрOHЃНOAЃЋAHЃН2ЃЋ3ЃН5ЃЌ
ЁпEHЁЭyжсЃЌEGЁЭxжсЃЌxжсЁЭyжсЃЌ
ЁрЫФБпаЮEGOHЮЊОиаЮЃЌ
ЁрEGЃНOHЃН5ЃЌOGЃНEHЃЌ
ЁпABЃН6ЃЌЁїABEЮЊЕШБпШ§НЧаЮЃЌЕуC1дкЁбEЩЯ
ЁрEC1ЃНEAЃНABЃН6ЃЌ
дкRtЁїEAHжаЃЌEH![]() ЃЌ
ЃЌ
ЁрOGЃНEHЃН![]() ЃЌ
ЃЌ
дкRtЁїEC1GжаЃЌC1G![]() ЃЌ
ЃЌ
ЁрOC1ЃН OGЃЋ C1GЃН![]() ЃЌ
ЃЌ
ЁрЕуC1зјБъЮЊ![]() ЃЌ
ЃЌ
ЭЌРэПЩЕУЃКЕуC2зјБъЮЊ![]() ЃЌ
ЃЌ
ТњзуЬѕМўЕФЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЌЕБЁбEгыxжсЯрЧагкЕуCЪБЃЌдђECЁЭxжсЃЌECЃНEBЃЌ

гжЁпEHЁЭyжсЃЌxжсЁЭyжсЃЌ
ЁрЫФБпаЮECOHЮЊОиаЮЃЌ
ЁрECЃНOHЃН5ЃЌ
ЁрEBЃНECЃН5ЃЌ
ЁрдкRtЁїEBHжаЃЌsinЁЯBEH![]() ЃЌ
ЃЌ
ЁпЁЯBEHЃН![]() ЁЯBEAЃЌЁЯACBЃН
ЁЯBEAЃЌЁЯACBЃН![]() ЁЯBEAЃЌ
ЁЯBEAЃЌ
ЁрЁЯACBЃНЁЯBEH
ЁрsinЁЯACBЃНsinЁЯBEH![]() ЃЌ
ЃЌ
ЁпЕБ![]() ЮЊШёНЧЪБЃЌТњзуЬѕМўЕФЕу
ЮЊШёНЧЪБЃЌТњзуЬѕМўЕФЕу![]() га4ИіЃЌ
га4ИіЃЌ
ЁрЁбEгыxжсЯрНЛЃЌ
ЁрsinЁЯACBЃМ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЕФШЁжЕЗЖЮЇЮЊЃК
ЕФШЁжЕЗЖЮЇЮЊЃК![]() ЃЎ
ЃЎ


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
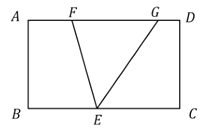
ЁОЬтФПЁПШчЭМЃЌдкОиаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊ
ЮЊ![]() БпЩЯвЛЖЏЕуЃЌ
БпЩЯвЛЖЏЕуЃЌ![]() ЁЂ
ЁЂ![]() ЮЊ
ЮЊ![]() БпЩЯСНИіЖЏЕуЃЌЧв
БпЩЯСНИіЖЏЕуЃЌЧв![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ЕФГЄЖШзюДѓжЕЮЊ__________ЃЎ
ЕФГЄЖШзюДѓжЕЮЊ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
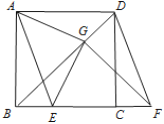
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧе§ЗНаЮ
ЪЧе§ЗНаЮ![]() ЕФЖдНЧЯпЃЌ
ЕФЖдНЧЯпЃЌ![]() ЃЌБп
ЃЌБп![]() дкЦфЫљдкжБЯпЩЯЯђгвЦНвЦЃЌНЋЭЈЙ§ЦНвЦЕУЕНЕФЯпЖЮМЧЮЊ
дкЦфЫљдкжБЯпЩЯЯђгвЦНвЦЃЌНЋЭЈЙ§ЦНвЦЕУЕНЕФЯпЖЮМЧЮЊ![]() ЃЌСЌНс
ЃЌСЌНс![]() ЃЌ
ЃЌ![]() ЃЌВЂЙ§Еу
ЃЌВЂЙ§Еу![]() зї
зї![]() ЃЌДЙзуЮЊ
ЃЌДЙзуЮЊ![]() ЃЌСЌНг
ЃЌСЌНг![]() КЭ
КЭ![]() ЃЌдкЦНвЦБфЛЛЙ§ГЬжаЃЌЩш
ЃЌдкЦНвЦБфЛЛЙ§ГЬжаЃЌЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]()
![]() ЃЌдђ
ЃЌдђ![]() ЕФзюДѓжЕЪЧ________ЃЎ
ЕФзюДѓжЕЪЧ________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпCЃКyЃН![]() гыжБЯпlЃКyЃНkx+bЯрНЛгкЕуAЃЌBЃЌжБЯпlгыyжсНЛгкЕуPЃЎ
гыжБЯпlЃКyЃНkx+bЯрНЛгкЕуAЃЌBЃЌжБЯпlгыyжсНЛгкЕуPЃЎ
ЃЈ1ЃЉЕБkЃН0ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЕуMЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуMзїMGЁЭжБЯпlгкЕуGЃЌЕБkЃН0ЪБЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ3ЃЉЕуMЪЧХзЮяЯпЩЯЕФЖЏЕуЃЌЙ§ЕуMзїMGЁЮyжсНЛжБЯпlгкЕуGЃЌЕБkЃН2ЪБЃЌЧѓжЄЃКВЛТлbЮЊКЮЪЕЪ§ЃЌ![]() ЕФжЕЮЊЖЈжЕЃЌВЂЧѓЖЈжЕЃЛ
ЕФжЕЮЊЖЈжЕЃЌВЂЧѓЖЈжЕЃЛ
ЃЈ4ЃЉШєНЋЃЈ2ЃЉЕФХзЮяЯпИФЮЊЁАyЃНax2ЁБЃЌЦфЫћЬѕМўВЛБфЃЌдђ![]() ЕФжЕЛЙЮЊЖЈжЕТ№ЃПШєЪЧЃЌЧыЧѓГіЖЈжЕЃЛШєВЛЪЧЃЌЫЕУїРэгЩЃЎ
ЕФжЕЛЙЮЊЖЈжЕТ№ЃПШєЪЧЃЌЧыЧѓГіЖЈжЕЃЛШєВЛЪЧЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФЖЅЕузјБъЗжБ№ЮЊAЃЈЉ6ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ8ЃЉЃЌАбЁїABCбижБЯпBCЗелЃЌЕуAЕФЖдгІЕуЮЊDЃЌХзЮяЯпy=ax2Љ10ax+cОЙ§ЕуCЃЌЖЅЕуMдкжБЯпBCЩЯЃЎ

ЃЈ1ЃЉжЄУїЫФБпаЮABCDЪЧСтаЮЃЌВЂЧѓЕуDЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФЖдГЦжсКЭКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉдкХзЮяЯпЩЯЪЧЗёДцдкЕуPЃЌЪЙЕУЁїPBDгыЁїPCDЕФУцЛ§ЯрЕШЃПШєДцдкЃЌжБНгаДГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§yЃНmx2ЉЃЈ2m+1ЃЉx+2ЃЈmЁй0ЃЉЃЌЧыХаЖЯЯТСаНсТлЪЧЗёе§ШЗЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ1ЃЉЕБmЃМ0ЪБЃЌКЏЪ§yЃНmx2ЉЃЈ2m+1ЃЉx+2дкxЃО1ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛ
ЃЈ2ЃЉЕБmЃО0ЪБЃЌКЏЪ§yЃНmx2ЉЃЈ2m+1ЃЉx+2ЭМЯѓНиxжсЩЯЕФЯпЖЮГЄЖШаЁгк2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЕуAдкЕквЛЯѓЯоЃЌBAЁЭyжсгкЕуBЃЌЗДБШР§КЏЪ§y=![]() ЃЈxЃО0ЃЉЕФЭМЯѓгыЯпЖЮABЯрНЛгкЕуCЃЌЧвCЪЧЯпЖЮABЕФжаЕуЃЌШєЁїOABЕФУцЛ§ЮЊ3ЃЌдђkЕФжЕЮЊ( )
ЃЈxЃО0ЃЉЕФЭМЯѓгыЯпЖЮABЯрНЛгкЕуCЃЌЧвCЪЧЯпЖЮABЕФжаЕуЃЌШєЁїOABЕФУцЛ§ЮЊ3ЃЌдђkЕФжЕЮЊ( )
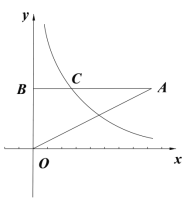
A.![]() B.1C.2D.3
B.1C.2D.3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЕФжаЕуЃЌСЌНг
ЕФжаЕуЃЌСЌНг![]() ЃЎНЋ
ЃЎНЋ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊ
ФцЪБеыЗНЯђа§зЊЃЌМЧа§зЊНЧЮЊ![]() ЃЎ
ЃЎ
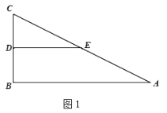

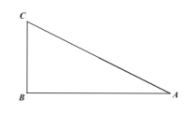
ЃЈ1ЃЉЮЪЬтЗЂЯж
ЂйЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ____________ЃЛЂкЕБ
____________ЃЛЂкЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ___________ЃЎ
___________ЃЎ
ЃЈ2ЃЉЭиеЙЬНОПЪдХаЖЯЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЕФДѓаЁгаЮоБфЛЏЃПЧыНіОЭЭМ2ЕФЧщаЮИјГіжЄУїЃЎ
ЃЈ3ЃЉЮЪЬтНтОі
![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊжС
ФцЪБеыа§зЊжС![]() Ш§ЕудкЭЌвЛЬѕжБЯпЩЯЪБЃЌжБНгаДГіЯпЖЮ
Ш§ЕудкЭЌвЛЬѕжБЯпЩЯЪБЃЌжБНгаДГіЯпЖЮ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
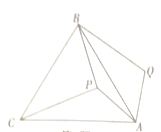
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧЕШБпШ§НЧаЮ
ЪЧЕШБпШ§НЧаЮ![]() ФквЛЕуЃЌНЋЯпЖЮ
ФквЛЕуЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ЕУЕНЯпЖЮ
ЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌдђЫФБпаЮ
ЃЌдђЫФБпаЮ![]() ЕФУцЛ§ЮЊЃЈ ЃЉ
ЕФУцЛ§ЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com