练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．下列运算正确的是（　　）
    A．2a-a=2B．2a+b=2abC．-a2b+2a2b=a2bD．3a2+2a2=5a4

    分析 利用合并同类项的运算法则运算即可．

    解答 解：A.2a-a=a，所以此选项错误；
    B.2a+b不能合并，所以此选项错误；
    C．-a2b+2a2b=a2b，所以此选项正确； 
    D.3a2+2a2=5a2，所以此选项错误，
    故选C．

    点评 本题主要考查了合并同类项，熟记运算法则：把同类项的系数相加，所得结果作为系数，字母和字母的指数不变是解答此题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    13．下列实数$\frac{2}{3}$，$\sqrt{3}$，$\root{3}{8}$，$\sqrt{4}$，$\frac{π}{3}$，0.1，-0.010010001…，0，2.333…，其中无理数共有（　　）
    A．2个B．3个C．4个D．5个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

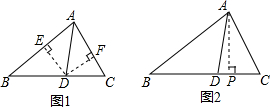    14．让我们来共同探究“三角形的角平分线”的特殊性质：
    如图，△ABC中，AD平分∠BAC，试探究S△ABD与S△ACD的比与图中线段有何关系．
    （1）下面（图1）是小明的做法，请你完成他的步骤：过点D作DE⊥AB，DF⊥AC，垂足分别为E、F．∵AD平分∠BAC，∴DE=DF．而S△ABD=$\frac{1}{2}$AB×DE，S△ACD=$\frac{1}{2}$AC×DF．则$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{（）}{（）}$；
    （2）下面（图2）是小华的做法，请你完成他的步骤：过点A作AP⊥BC，垂足为P，而S△ABD=$\frac{1}{2}$×BD×AP，S△ACD=$\frac{1}{2}$×CD×AP，则$\frac{{S}_{△ABD}}{{S}_{△ACD}}$=$\frac{（）}{（）}$
    （3）结合（1）、（2）的结论，可得“三角形的角平分线”的一个新的性质：
    已知：在△ABC中，AD平分∠BAC，则线段AB、AC、BD、CD的关系为：$\frac{AB}{AC}$=$\frac{BD}{CD}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．如果关于x的一元二次方程ax2+bx+c=0有两个实数根，且其中一个实数根为另一个实数根的3倍，则称这样的方程为“立根方程”．
    若方程ax2+bx+c=0是立根方程，且两点P（p+p2+1，q）、Q（-p2+5+q，q）均在二次函数y=ax2+bx+c上，请求方程ax2+bx+c=0的两个根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．如图，在∠A=30°的等腰三角形ABC中，AB=AC，若过点C作CD⊥AB于点D，则∠BCD=15°．根据图形，计算tan15°的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．计算：$\frac{1}{2-a}$+$\frac{1}{2+a}$-$\frac{{a}^{2}-4a}{{a}^{2}-4}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列等式是一元一次方程的是（　　）
    A．x2+3x=6B．2x=4C．-$\frac{1}{2}$x-y=0

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下面①②③④用拼图法验证“三角形内角和为180°”，能成为证明这个定理思路的有（　　）
    A．①②③④B．①③C．③④D．①②

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列事件中，是必然事件的是（　　）
    A．打开电视机，它正在直播排球比赛
    B．抛掷5枚硬币，结果是2个正面朝上与3个反面朝上
    C．黑暗中从一大串钥匙中随便选中一把，用它打开了门
    D．投掷一枚普通的正方体骰子，正面朝上的数不是奇数便是偶数

    查看答案和解析>>

    同步练习册答案