
【题目】如图,AE=AF,AB=AC,EC与BF交于点O,∠A=60°,∠B=25°,求∠EOB的度数.
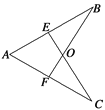
【答案】∠EOB=70°.
【解析】
利用SAS可证明△ABF≌△ACE,根据全等三角形的对应角相等可得∠B=∠C,根据三角形外角的性质得到∠BFC=∠A+∠B,求出∠BFC的度数,在△FOC中,根据三角形的内角和定理求出∠COF的度数,最后根据对顶角相等可得∠EOB的度数.
在△ABF和△ACE中,
∵AF=AE,∠A=∠A,AB=AC,
∴△ABF≌△ACE(SAS).
∴∠B=∠C.
∵∠B=25°,∴∠C=25°.
又∵∠CFB是△AFB的外角,∠A=60°,
∴∠CFB=60°+25°=85°,
∴∠COF=180°-∠CFB-∠C=180°-85°-25°=70°.
又∵∠EOB=∠COF,∴∠EOB=70°.


科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,抛物线y=x2﹣2mx+m2+![]() m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
m的顶点为A,与y轴交于点B.当抛物线不经过坐标原点时,分别作点A、B关于原点的对称点C、D,连结AB、BC、CD、DA.
(1)分别用含有m的代数式表示点A、B的坐标.
(2)判断点B能否落在y轴负半轴上,并说明理由.
(3)连结AC,设l=AC+BD,求l与m之间的函数关系式.
(4)过点A作y轴的垂线,交y轴于点P,以AP为边作正方形APMN,MN在AP上方,如图②,当正方形APMN与四边形ABCD重叠部分图形为四边形时,直接写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,AB=6,∠DBC=30°,DM平分∠BDC交BC于M,△EFG中,∠F=90°,GF= ![]() ,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒
,∠E=30°,点F、G、B、C共线,且G、B重合,△EFG沿折线B﹣M﹣D方向以每秒 ![]() 个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
个单位长度平移,得到△E1F1G1 , 平移过程中,点G1始终在折线B﹣M﹣D上,△E1F1G1与△DBM无重叠时,△E1F1G1停止运动,设△E1F1G1与△DBM重叠部分面积为S,平移时间为t,
(1)当△E1F1G1的顶点G1恰好在BD上时,t=秒;
(2)直接写出S与t的函数关系式,及自变量t的取值范围;
(3)如图2,△E1F1G1平移到G1与M重合时,将△E1F1G1绕点M旋转α°(0°<α<180°)得到△E2F2G1 , 点E1、F1分别对应E2、F2 , 设直线F2E2与直线DM交于P,与直线DC交于Q,是否存在这样的α,使△DPQ为直角三角形?若存在,求α的度数和DQ的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AD平分∠CAB.
(1)求∠CAD的度数;
(2)延长AC至E,使CE=AC,求证:DA=DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,
与x轴相交于点A、B,与y轴相交于点C,抛物线对称轴与x轴相交于点M,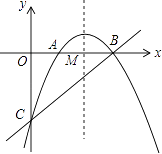
(1)求△ABC的面积;
(2)若p是x轴上方的抛物线上的一个动点,求点P到直线BC的距离的最大值;
(3)若点P在抛物线上运动(点P异于点A),当∠PCB=∠BCA时,求直线PC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,已知AD>AB,在边AD上取点E,连结CE,过点E作EF⊥CE,与边AB的延长线交于点F. 
(1)证明:△AEF∽△DCE.
(2)若AB=2,AE=3,AD=7,求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10,将△APB绕点B逆时针旋转一定角度后,可得到△CQB. 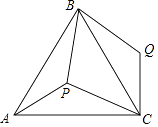
(1)求点P与点Q之间的距离;
(2)求∠APB的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com