
分析 首先把分式的分子分母分解因式,约分化简,再代入$\frac{b}{a}$=$\frac{1}{2}$,即可.
解答 解:$\frac{{a}^{2}-{b}^{2}}{{a}^{2}-ab}$=$\frac{(a+b)(a-b)}{a(a-b)}$=$\frac{a+b}{a}$=1+$\frac{b}{a}$
当$\frac{a}{b}$=2时,$\frac{b}{a}$=$\frac{1}{2}$,故原式═1+$\frac{1}{2}$=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 此题主要考查了分式的值,在解答时应从已知条件和所求问题的特点出发,通过适当的变形、转化,才能发现解题的捷径.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
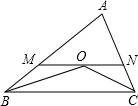 如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )
如图,△ABC中,∠ABC、∠ACB的平分线相交于O,MN过点O且与BC平行.△ABC的周长为20,△AMN的周长为12,则BC的长为( )| A. | 10 | B. | 16 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
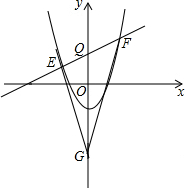 如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.
如图,抛物线y=$\frac{1}{2}$x2-2交y轴于C,不平行于x轴的直线y=kx+3交抛物线于E、F,交y轴于点Q,在y轴的负半轴上是否存在点G使EQ•FG=FQ•EG,若存在,请求出G点坐标;若不存在.请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com