
【题目】如图,点A是反比例函数y=﹣ ![]() 在第二象限内图象上一点,点B是反比例函数y=
在第二象限内图象上一点,点B是反比例函数y= ![]() 在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
在第一象限内图象上一点,直线AB与y轴交于点C,且AC=BC,连接OA、OB,求△AOB的面积.
【答案】解:分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,
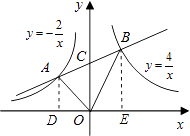
∵AC=CB,∴OD=OE,
设A(﹣a, ![]() ),则B(a,
),则B(a, ![]() ),
),
故S△AOB=S梯形ADBE﹣S△AOD﹣S△BOE
= ![]() (
( ![]() +
+ ![]() )×2a﹣
)×2a﹣ ![]() a×
a× ![]() ﹣
﹣ ![]() a×
a× ![]() =3.
=3.
【解析】分别过A、B两点作AD⊥x轴,BE⊥x轴,垂足为D、E,可证明AD∥OC∥BE,由AC=CB,根据平行线等分线段,得出OD=OE,设出点A、B的坐标,由S△AOB=S梯形ADBE﹣S△AOD﹣S△BOE即可求出结果。
【考点精析】通过灵活运用直角梯形和平行线分线段成比例,掌握一腰垂直于底的梯形是直角梯形;三条平行线截两条直线,所得的对应线段成比例即可以解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】(1)如图①在△ABC中,点D是BC边上的一点,将△ABD沿AD折叠,得到△AED,AE与BC交于点F.已知∠B=50°,∠BAD=15°,求∠AFC的度数.
(2)如图②,将△ABC纸片沿DE折叠,使点A落在四边形BCED的内部点A′的位置,∠1、∠2与∠A之间存在一定的数量关系,请判断它们之间的关系,并说明理由.
(3)如图③,将△ABC纸片沿DE折叠,使点A落在四边形BCED的外部点A′的位置,此时∠1、∠2与∠A之间也存在一定的数量关系,请直接写出它们之间的关系,无需说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用两个边长为15![]() 的小正方形拼成一个大的正方形,
的小正方形拼成一个大的正方形,
(1)求大正方形的边长?
(2)若沿此大正方形边的方向剪出一个长方形,能否使剪出的长方形纸片的长宽之比为4:3,且面积为720cm2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前我市“校园手机”现象越来越受到社会关注,针对这种现象,随机抽查了某中学九年级的同学,关于手机在中学生中的主要用途做了调查,对调查数据进行统计整理、制作了如下的两种统计图,请根据图形回答问题: 
(1)这次被调查的学生共有人,其中主要用于“上网聊天”的学生人数占抽样人数的百分比为;
(2)请你将条形统计图(2)补充完整;
(3)若该校共有3000名学生,请你估计主要使用手机玩游戏的人数大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下四个命题,其中原命题与逆命题均为真命题的个数是( )
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③角的平分线上的点到角的两边的距离相等;
④线段的垂直平分线上的点到线段两端点距离相等.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有点A(1,0),点A第一次跳动至点![]() ,第二次点
,第二次点![]() 跳动至点
跳动至点![]() 第三次点
第三次点![]() 跳动至点
跳动至点![]() ,第四次点
,第四次点![]() 跳动至点
跳动至点![]() ……,依此规律跳动下去,则点
……,依此规律跳动下去,则点![]() 与点
与点![]() 之间的距离是( )
之间的距离是( )

A. 2017B. 2018C. 2019D. 2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,D为△ABC所在平面内的一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB于点E,F.
(1)如图1,当点D在线段BC上时,通过观察分析线段DE、DF、AB之间的数量关系,并说明理由;
(2)如图2,当点D在直线BC上,其他条件不变时,试猜想线段DE、DF、AB之间的数量关系(请直接写出等式,不需证明);
(3)如图3,当点D是△ABC内一点,过D作DE∥AB,DF∥AC分别交直线AC,直线AB和直线BC于E、F和G. 试猜想线段DE、DF、DG与AB之间的数量关系(请直接写出等式,不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果商在批发市场按每千克1.5元批发了若干千克的西瓜进城出售,为了方面他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜的重量![]() (千克)与他手中持有的钱数
(千克)与他手中持有的钱数![]() (元)(含备用零钱)的关系如图所示,结合图象回答下列问题:
(元)(含备用零钱)的关系如图所示,结合图象回答下列问题:
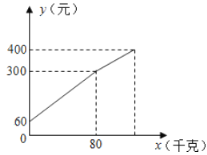
(1)水果商自带的零钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元的价格将剩余的西瓜售完,这时他手中的钱(含备用零钱)是400元,他一共批发了多少千克的西瓜?
(4)这个水果商一共赚了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com