
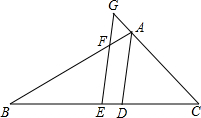
 如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.求证:BF=AC+AF.
如图,在△ABC中,AB>AC,E为BC边的中点,AD为∠BAC的平分线,过E作AD的平行线,交AB于F,交CA的延长线于G.求证:BF=AC+AF. 分析 延长FE至Q,使EQ=EF,连接CQ,根据SAS证△BEF≌△CEQ,推出BF=CQ,∠BFE=∠Q,根据平行线性质和角平分线性质推出∠G=∠GFA=∠BFE,推出∠G=∠Q,推出CQ=CG即可.
解答 证明: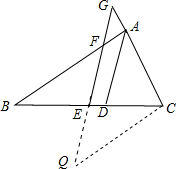 延长FE至Q,使EQ=EF,连接CQ,
延长FE至Q,使EQ=EF,连接CQ,
∵E为BC边的中点,
∴BE=CE,
∵在△BEF和△CEQ中$\left\{\begin{array}{l}{BE=CE}\\{∠BEF=∠CEQ}\\{EF=EQ}\end{array}\right.$,
∴△BEF≌△CEQ,
∴BF=CQ,∠BFE=∠Q,
∵AD平分∠BAC,
∴∠CAD=∠BAD,
∵EF∥AD,
∴∠CAD=∠G,∠BAD=∠GFA,
∴∠G=∠GFA,
∴∠GFA=∠BFE,AG=AF,
∵∠BFE=∠Q(已证),
∴∠G=∠Q,
∴CQ=CG,
∵CQ=BF,
∴BF=CG=AG+AC=AF+AC.
点评 本题考查了全等三角形的性质和判定,平行线的性质和角平分线性质的应用,主要考查学生运用性质进行推理的能力,正确作辅助线是解此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
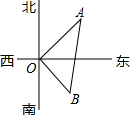 如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )
如图,在水塔O的东北方向32m处有一抽水站A,在水塔的东南方向24m处有一建筑工地B,在AB间建一条直水管,则水管的长为( )| A. | 45m | B. | 40m | C. | 50m | D. | 56m |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
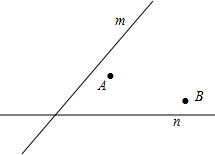 如图,移动公司要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也相等,请用尺规作图法作出发射塔P的位置.(保留作图痕迹)
如图,移动公司要在S区修建一座信号发射塔,按照设计要求,发射塔到两个城镇A、B的距离相等,到两条高速公路m和n的距离也相等,请用尺规作图法作出发射塔P的位置.(保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 |
| -5 | +7 | -9 | +10 | +6 | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
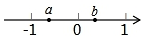 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2.
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com