
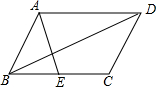
 如图,在平行四边形ABCD中,AD=10,BD=12,点E为BC边上任意一点,连接AE、DE,当AE=5,BE=3时,平行四边形ABCD的面积是$\frac{600}{13}$.
如图,在平行四边形ABCD中,AD=10,BD=12,点E为BC边上任意一点,连接AE、DE,当AE=5,BE=3时,平行四边形ABCD的面积是$\frac{600}{13}$. 分析 过点A作AM⊥BC于点M,过点D作DN⊥BC的延长线于点N,设BM=a,AM=b,则ME=3-a,DN=AM=b,BN=10+a.在Rt△AME和Rt△BND中,由勾股定理即可得出关于a、b的二元二次方程组,解方程组即可得出b值,再根据平行四边形的面积公式即可得出结论.
解答 解:过点A作AM⊥BC于点M,过点D作DN⊥BC的延长线于点N,如图所示.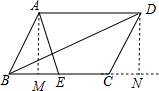
设BM=a,AM=b,则ME=3-a,DN=AM=b,BN=10+a.
在Rt△AME中,AM2=AE2-ME2=52-(3-a)2=b2①;
在Rt△BND中,DN2=BD2-BN2=122-(10+a)2=b2②.
联立①②得:$\left\{\begin{array}{l}{25-(3-a)^{2}={b}^{2}}\\{144-(10+a)^{2}={b}^{2}}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=\frac{14}{13}}\\{b=\frac{60}{13}}\end{array}\right.$或$\left\{\begin{array}{l}{a=\frac{14}{13}}\\{b=-\frac{60}{13}}\end{array}\right.$(舍去).
S平行四边形ABCD=AD•AM=10×$\frac{60}{13}$=$\frac{600}{13}$.
故答案为:$\frac{600}{13}$.
点评 本题考查了平行四边形的性质、勾股定理以及解二元二次方程组,解题的关键是求出边BC上的高AM的长度.本题属于中档题,难度不大,解决该题型题目时,借助于勾股定理得出方程组是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com