
【题目】如图,∠AOB=90°,C在OB的延长线上,D为⊙O上一点,∠BAD=∠BDC.
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为1,且OB=BC,求四边形AOBD的面积.

【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)作直径BE,连接OD、DE,如图,利用圆周角定理得到∠BDE=90°,∠E=∠BAD,由于∠BAD=∠BDC.则∠E=∠BDC,加上∠DBO=∠BDO,则∠BDC+∠BDO=90°,然后根据切线的判定定理可得到CD是⊙O的切线;
(2)先根据直角斜边上中线性质得DB=OB=OD,则△OBD为等边三角形,所以S△OBD=![]() ,
,
∠BOD=60°,再作DF⊥OA于F,如图,则DF=![]() OD=
OD=![]() ,所以S△ODA=
,所以S△ODA=![]() ,然后利用四边形AOBD的面积=S△OBD+S△ODA进行计算即可.
,然后利用四边形AOBD的面积=S△OBD+S△ODA进行计算即可.
试题解析:
(1)证明:作直径BE,连接OD、DE,如图,
∵BE为直径,
∴∠BDE=90°,
∴∠DBE+∠E=90°,
∵∠E=∠BAD,∠BAD=∠BDC,
∴∠E=∠BDC,
∵OB=OD,
∴∠DBO=∠BDO,
∴∠BDC+∠BDO=90°,即∠CDO=90°,
∴OD⊥CD,
∴CD是⊙O的切线.
(2)解:∵OB=CB,
∴BD为直角△ODC的斜边OC的中线,
∴DB=OB=OD,
∴△OBD为等边三角形,
∴S△OBD=![]() OB2=
OB2=![]() ,∠BOD=60°,
,∠BOD=60°,
∵OA⊥OB,
∴∠AOD=30°,
作DF⊥OA于F,如图,
在Rt△ODF中,DF=![]() OD=
OD=![]() ,
,
∴S△ODA=![]() 1
1![]() =
=![]() ,
,
∴四边形AOBD的面积=S△OBD+S△ODA=![]() +
+![]() =
=![]() .
.



科目:初中数学 来源: 题型:
【题目】出租车司机小张某天上午劳动线路是在南北走向的公路上进行的,如果规定向南为正,向北为负,他这天上午行车里程(单位:千米)如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)将最后一名乘客送到目的地时,小张距上午出发时的出发点多远?在出发点的南边还是北边?
(2)若汽车耗油量为![]() 升/千米,这天上午汽车耗油多少升?
升/千米,这天上午汽车耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知ΔABC是边长为1的等腰直角三角形,以RtΔABC的斜边AC为直角边,画第二个等腰RtΔACD,再以RtΔACD的斜边AD为直角边,画第三个等腰RtΔADE,……
如此类推.(直接写出结果)

(1)AC的长 、AE的长 ;
(2)第n个等腰直角三角形的斜边长 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点D的坐标是(-3,1),点A的坐标是(4,3).

(1)将△ABC平移后使点C与点D重合,点A、B与点E、F重合,画出△DEF,并直接写出E、F的坐标.
(2)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为多少?
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
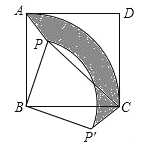
【题目】已知:如图,点P是正方形ABCD内一点,连接PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°得到△P'CB,若AB=m,PB=n(n<m).求△PAB旋转过程中边PA扫过区域(阴影部分)的面积;
(2)若PA=![]() ,PB=
,PB=![]() ,∠APB=135°,求PC的长.
,∠APB=135°,求PC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应党的“文化自信”号召,某校开展了古诗词诵读大赛活动,现随机抽取部分同学的成绩进行统计,并绘制成如下的两个不完整的统计图,请结合图中提供的信息,解答下列问题:

(1)填空:样本容量为________,![]() ________;
________;
(2)把频数分布直方图补充完整;
(3)求扇形![]() 的圆心角度数;
的圆心角度数;
(4)如果全校有2000名学生参加这次活动,90分以上(含90分)为优秀,那么估计获得优秀奖的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学组织春游活动,到超市选购A, B两种饮料,若购买6瓶A种饮料, 4瓶B种饮料需花费39元,购买20瓶A种饮料和30瓶B种饮料需花费180元。
(1)购买A, B两种饮料每瓶各多少元?
(2)实际购买时,恰好超市进行促销活动,如果一次性购买 A种饮料数量超过20瓶,则超出部分的价格享受八折优惠,B种饮料价格保持不变,若购买B种饮料的数量是A种饮料数量的2倍还多10瓶,且总费用不超过320元则最多可购买A种饮料多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;(其中A1、B1、C1分别是A、B、C的对应点,不写画法.)
(2)写出点A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com