
【题目】某电视台摄制组乘船往返于A码头和B码头进行拍摄,在A、B两码头间设置拍摄中心C.在往返过程中,假设船在A、B、C处均不停留,船离开B码头的距离s(千米)与航行的时间t(小时)之间的函数关系式如图所示.根据图象信息,解答下列问题:
(1)求船从B码头返回A码头时的速度及返回时s关于t的函数表达式.
(2)求水流的速度.
(3)若拍摄中心C设在离A码头12千米处,摄制组在拍摄中心分两组拍摄,其中一组乘橡皮艇漂流到B码头处,另一组同时乘船到达A码头后马上返回,求两摄制组相遇时离拍摄中心C的距离.

【答案】(1)s=9t;(2)4.5千米/时;(3)12千米
【解析】
(1)根据题意,船从B码头返回A码头时的速度27÷3=9千米/时,
设返回时s关于t的函数表达式为s=kt,过(3,27),即可得出k=9,进而求出s关于t的函数表达式为s=9t (0≤t≤3)
(2)首先分别求出船由B到A的速度和由A到B的速度,再根据:顺水速﹣逆水速=水速的2倍即可得出水流的速度;
(3)首先求出当船到达A地用时,再求出此时橡皮艇行至距C地的距离,设船从A返回追橡皮艇时间为x时,则可得出18x=4.5x+12+6,解得x=![]() ,即可求出此时距C的距离.
,即可求出此时距C的距离.
解:(1)船从B码头返回A码头时的速度27÷3=9千米/时,
设返回时s关于t的函数表达式为s=kt,过(3,27)
∴k=9
∴s关于t的函数表达式为s=9t (0≤t≤3)
答:船从B码头返回A码头时的速度为9千米/时,返回时s关于t的函数表达式为:s=9t.
(2)船由B到A的速度为:27÷3=9千米/时,由A到B的速度为:27÷(4.5﹣3)=18千米/时,
根据:顺水速﹣逆水速=水速的2倍得:(18﹣9)÷2=4.5千米/时,
故水流的速度为4.5千米/时;
(3)当船到达A地用时为:12÷9=![]() 时,此时橡皮艇行至距C地4.5×
时,此时橡皮艇行至距C地4.5×![]() =6千米处,
=6千米处,
设船从A返回追橡皮艇时间为x时,则:18x=4.5x+12+6
解得:x=![]()
此时距C的距离为:4.5×(![]() +
+![]() )=12千米.
)=12千米.
答:两摄制组相遇时离拍摄中心C的距离为12千米.


科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,如果按每件10元出售,那么每天可销售100件,经调查发现,这种商品的销售单价每提高1元,其销售量相应减少10件.
(1)求销售量![]() 件与销售单价
件与销售单价![]() 元之间的关系式;
元之间的关系式;
(2)当销售单价![]() 定为多少,才能使每天所获销售利润最大?最大利润是多少?
定为多少,才能使每天所获销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
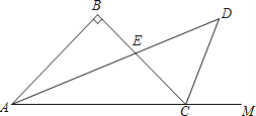
【题目】如图,在△ABC中,∠B=90°,AB=BC,∠BCM是△ABC的外角,∠BAC、∠BCM的平分线交于点D,AD与BC交于点E,若BE=2,则AEDE=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
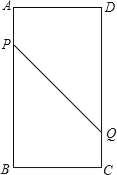
【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB以3cm/s的速度向点B移动(不与点A,B重合);同时点Q从点C出发沿CD以2cm/s的速度向点D移动(不与点C、D重合),经过几秒,△PDQ为直角三角形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:![]() ,其中|x|≤1,且x为整数.
,其中|x|≤1,且x为整数.
小海同学的解法如下:
解:原式=![]() ﹣
﹣![]() ①
①
=(x﹣1)2﹣x2+3 ②
=x2﹣2x﹣1﹣x2+3 ③
=﹣2x+2.④
当x=﹣1时,⑤
原式=﹣2×(﹣1)+2⑥
=2+2=4.⑦
请指出他解答过程中的错误(写出相应的序号,多写不给分),并写出正确的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张背面完全相同的卡片,正面上分别标有数字﹣2,﹣1,1,2.把这四张卡片背面朝上,随机抽取一张,记下数字为m;放回搅匀,再随机抽取一张卡片,记下数字为n,则y=mx+n不经过第三象限的概率为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,等腰Rt△ABC中,∠ACB=90°,CB=CA,在△ABE中,∠AEB=90°,AE与BC交于点F.
(1)若∠BAE=30°,BF=2![]() ,求BE的长;
,求BE的长;
(2)如图2,D为BE延长线上一点,连接AD、FD、CD,若AB=AD,∠ACD=135°,求证:BD+BF=AF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B、C重合的一个动点,把△EBF沿EF折叠,点B落在B′处,若△CDB′恰为等腰三角形,则DB′的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com