
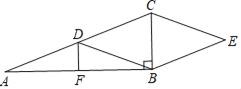
【题目】如图,Rt△ABC中,∠ABC=90°,点D,F分别是AC,AB的中点,CE∥DB,BE∥DC.
(1)求证:四边形DBEC是菱形;
(2)若AD=3,DF=1,求四边形DBEC面积.

【答案】(1)见解析;(2)4![]()
【解析】分析:(1)根据平行四边形的判定定理首先推知四边形DBEC为平行四边形,然后由直角三角形斜边上的中线等于斜边的一半得到其邻边相等:CD=BD,得证;
(2)由三角形中位线定理和勾股定理求得AB边的长度,然后根据菱形的性质和三角形的面积公式进行解答.
详解:(1)证明:∵CE∥DB,BE∥DC,
∴四边形DBEC为平行四边形.
又∵Rt△ABC中,∠ABC=90°,点D是AC的中点,
∴CD=BD=![]() AC,
AC,
∴平行四边形DBEC是菱形;
(2)∵点D,F分别是AC,AB的中点,AD=3,DF=1,
∴DF是△ABC的中位线,AC=2AD=6,S△BCD=![]() S△ABC
S△ABC
∴BC=2DF=2.
又∵∠ABC=90°,
∴AB=![]() =
=![]() =4
=4![]() .
.
∵平行四边形DBEC是菱形,
∴S四边形DBEC=2S△BCD=S△ABC=![]() ABBC=
ABBC=![]() ×4
×4![]() ×2=4
×2=4![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点 B 以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点再以每秒2个单位长度沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的三边为边分别作等边△ACD、△ABE、△BCF, 则下列结论:
①△EBF≌△DFC;
②四边形AEFD为平行四边形;
③当AB=AC,∠BAC=1200时,四边形AEFD是正方形.
其中正确的结论是 .(请写出正确结论的番号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在边AD上,点F在边BC的延长线上,连结EF与边CD相交于点G,连结BE与对角线AC相交于点H,AE=CF,BE=EG.

(1)求证:EF∥AC;
(2)求∠BEF大小;
查看答案和解析>>
科目:初中数学 来源: 题型:
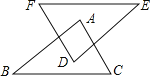
【题目】如图,AB∥DE,AC∥DF,AC=DF,添加下列条件,不能判断 △ABC≌△DEF的是( )
A. EF=BC B. AB=DE C. EF∥BC D. ![]() B=
B=![]() E
E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,港口A在观测站O的正东方向,OA=6km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为( )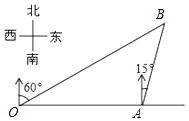
A.3 ![]() km
km
B.3 ![]() km
km
C.4 km
D.(3 ![]() ﹣3)km
﹣3)km
查看答案和解析>>
科目:初中数学 来源: 题型:
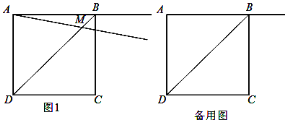
【题目】正方形ABCD的边长为2,过点A作射线AM与线段BD交于点M,∠BAM=α(0°<α<90°),作CE⊥AM于点E,点N与点M关于直线CE对称,连接CN.
(1)如图①,当0°<α<45°时,
①依题意在图①中补全图并证明:AM=CN ②当BD∥CN,求DM的值
(2)探究∠NCE与∠BAM之间的数量关系并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究多边形内角和问题.
连接多边形不相邻的两个顶点的线段叫做多边形的对角线.从多边形某一个顶点出发的×对角线可以把一个多边形分成几个三角形.这样就把多边形内角和问题转化为三角形内角和问题了.
(1)请你试一试,做一做,把下面表格补充完整:
名称 | 图形 | 内角和 |
三角形 |
| 180° |
四边形 |
| 2×180°=360° |
五边形 |
|
|
六边形 |
|
|
… | … | … |
根据表格探究发现的规律,完成下面的问题:
(2)七边形的内角和等于 度;
(3)如果一个多边形有n条边,请你用含有n的代数式表示这个多边形的内角和: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若顺次连接四边形的各边中点所得的四边形是菱形,则该四边形一定是( )
A. 矩形 B. 一组对边相等,另一组对边平行的四边形
C. 对角线互相垂直的四边形 D. 对角线相等的四边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com