
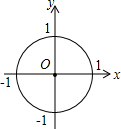
 如图,在直角坐标系中,⊙O的半径是1,则直线y=-x+$\sqrt{2}$与⊙O的位置关系是( )
如图,在直角坐标系中,⊙O的半径是1,则直线y=-x+$\sqrt{2}$与⊙O的位置关系是( )| A. | 相离 | B. | 相交 | ||
| C. | 相切,切点在第二象限 | D. | 相切,切点在第一象限 |
分析 如图,要判断直线与圆的位置关系,只要求出圆心到直线的距离;为此,首先求出OA、OB的长度,进而求出AB的长度;证明OC⊥AB,此为解题的关键性结论;求出OC的长,即可解决问题.
解答 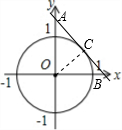 解:如图,对于直线y=-x+$\sqrt{2}$,
解:如图,对于直线y=-x+$\sqrt{2}$,
当x=0时,y=$\sqrt{2}$,当y=0时,x=$\sqrt{2}$,
∴OA=$\sqrt{2}$,OB=$\sqrt{2}$,
△AOB为等腰直角三角形;取AB的中点C,连接OC;
则OC=$\frac{1}{2}$AB,且OC⊥AB;
由勾股定理得:AB=$\sqrt{(\sqrt{2})^{2}+(\sqrt{2})^{2}}$=2,
∴OC=1,即圆心O到直线的距离等于圆的半径,
∴直线y=-x+$\sqrt{2}$与⊙O的位置关系是相切,
切点在第一象限.
故选D.
点评 该题主要考查了直线与圆的位置关系的判定及其应用问题;解题的关键是准确求出圆心到直线的距离,进而比较距离与半径的大小关系.


科目:初中数学 来源: 题型:选择题
 将一圆形纸片对折后再对折,得到如图所示,然后沿着图中的虚线剪去一个角(即△OMN),再将余下部分展开后的平面后的平面图形是( )
将一圆形纸片对折后再对折,得到如图所示,然后沿着图中的虚线剪去一个角(即△OMN),再将余下部分展开后的平面后的平面图形是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
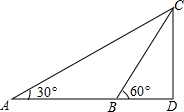 为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为30°,然后他向气球方向前进了40m,此时观测气球,测得仰角为60°,如图,点A、B表示小明两次观测气球时眼睛的位置,若小明的眼睛离地面1.5m,请你帮助他计算出气球的高度.(结果保留根号)
为了测量停留在空中的气球的高度,小明先站在地面上某点处观测气球,测得仰角为30°,然后他向气球方向前进了40m,此时观测气球,测得仰角为60°,如图,点A、B表示小明两次观测气球时眼睛的位置,若小明的眼睛离地面1.5m,请你帮助他计算出气球的高度.(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com