
【题目】(6分)如图,菱形ABCD的对角线AC,BD相交于点O,分别延长OA,OC到点E,F,使AE=CF,依次连接B,F,D,E各点.

(1)求证:△BAE≌△BCF;
(2)若∠ABC=50°,则当∠EBA= °时,四边形BFDE是正方形.
【答案】(1)证明见试题解析;(2)20.
【解析】
试题(1)先证∠BAE=∠BCF,又由BA=BC,AE=CF,得到△BAE≌△BCF;
(2)由已知可得四边形BFDE对角线互相垂直平分,只要∠EBF=90°即得四边形BFDE是正方形,由△BAE≌△BCF可知∠EBA=∠FBC,又由∠ABC=50°,可得∠EBA+∠FBC=40°,于是∠EBA=![]() ×40°=20°.
×40°=20°.
试题解析:(1)∵菱形ABCD的对角线AC,BD相交于点O,∴AB=BC,∠BAC=∠BCA,∴∠BAE=∠BCF,在△BAE与△BCF中,∵BA=BC,∠BAE=∠BCF,AE=CF,∴△BAE≌△BCF(SAS);
(2)∵四边形BFDE对角线互相垂直平分,∴只要∠EBF=90°即得四边形BFDE是正方形,∵△BAE≌△BCF,∴∠EBA=∠FBC,又∵∠ABC=50°,∴∠EBA+∠FBC=40°,∴∠EBA=![]() ×40°=20°.故答案为:20.
×40°=20°.故答案为:20.


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】给出如下四个命题,其中原命题与逆命题均为真命题的个数是( )
①若![]() ,
,![]() ,则
,则![]() ;
;
②若![]() ,则
,则![]() ;
;
③角的平分线上的点到角的两边的距离相等;
④线段的垂直平分线上的点到线段两端点距离相等.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:我们在学习二次根式时,式子![]() 有意义,则x≥0;式子
有意义,则x≥0;式子![]() 有意义,则x≤0;若式子
有意义,则x≤0;若式子![]() +
+![]() 有意义,求x的取值范围. 这个问题可以转化为不等式组来解决,即求关于x的不等式组x≥0,x≤0的解集,解这个不等式组,得x=0. 请你运用上述的数学方法解决下列问题:
有意义,求x的取值范围. 这个问题可以转化为不等式组来解决,即求关于x的不等式组x≥0,x≤0的解集,解这个不等式组,得x=0. 请你运用上述的数学方法解决下列问题:
(1)式子![]() +
+![]() 有意义,求x的取值范围;
有意义,求x的取值范围;
(2)已知y=![]() +
+![]() -3,求
-3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
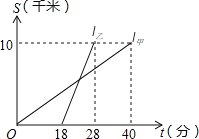
【题目】甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t(分)变化的函数图象.以下说法:
①乙比甲提前12分钟到达; ②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲; ④乙出发6分钟后追上甲.
其中正确的有_____________(填所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果商在批发市场按每千克1.5元批发了若干千克的西瓜进城出售,为了方面他带了一些零钱备用.他先按市场价售出一些后,又降价出售.售出西瓜的重量![]() (千克)与他手中持有的钱数
(千克)与他手中持有的钱数![]() (元)(含备用零钱)的关系如图所示,结合图象回答下列问题:
(元)(含备用零钱)的关系如图所示,结合图象回答下列问题:
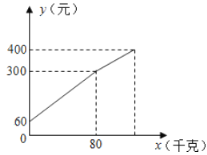
(1)水果商自带的零钱是多少?
(2)降价前他每千克西瓜出售的价格是多少?
(3)随后他按每千克下降0.5元的价格将剩余的西瓜售完,这时他手中的钱(含备用零钱)是400元,他一共批发了多少千克的西瓜?
(4)这个水果商一共赚了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,教师出示某区篮球赛积分表如下:

(1)从表中可以看出,负一场积多少分,胜一场积多少分;
(2)请你帮忙算出二队胜了多少场?
(3)在这次比赛中,一个队胜场总积分能不能等于它的负场总积分?
(4)在计算五队、六队胜出场次的时候,老师还没等同学们计算出来就立刻说出了答案,老师解释说:“我是通过找到积分与胜场之间的数量关系求出来的”,请你说出其中的奥秘.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径,CD为⊙O的弦,CD∥AB,过点B的切线与射线AD交于点M,连接AC,BD.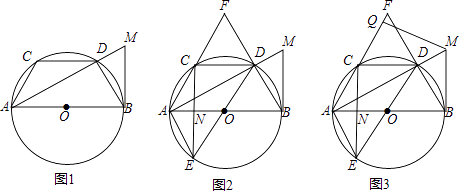
(1)如图l,求证:AC=BD;
(2)如图2,延长AC、BD交于点F,作直径DE,连接AE、CE,CE与AB交于点N,求证:∠AFB=2∠AEN;
(3)如图3,在(2)的条件下,过点M作MQ⊥AF于点Q,若MQ:QC=3:2,NE=2,求QF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com