
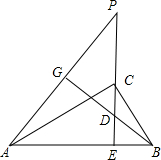
 如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE.
如图,CE是直角△ABC斜边AB上的高,在EC的延长线上任取一点P,连接AP,过B作BG⊥AP于G,交CE于D,求证:CE2=PE•DE. 分析 首先证Rt△ACE∽Rt△CBE,得出CE2=AE•BE(即射影定理);再通过证△AEP∽△BED,得出PE•DE=AE•BE,联立上述两式即可得出本题要证的结论.
解答 证明:
∵∠ACB=90°,CE⊥AB,
∴∠ACE+∠BCE=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCE,
∴Rt△ACE∽Rt△CBE;
∴$\frac{CE}{BE}=\frac{AE}{CE}$;
∴CE2=AE•BE;
又∵BG⊥AP,CE⊥AB,
∴∠DEB=∠DGP=∠PEA=90°,
∵∠1=∠2,
∴∠P=∠3,
∴△AEP∽△DEB,
∴$\frac{PE}{BE}=\frac{AE}{DE}$,
∴PE•DE=AE•BE,
∴CE2=PE•DE.
点评 此题主要考查的是相似三角形的判定和性质,关键是根据相似三角形的判定证Rt△ACE∽Rt△CBE.


 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:解答题
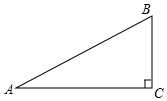 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com