
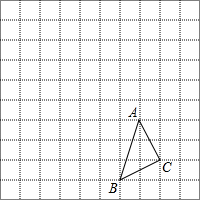
 △ABC在方格中的位置如图所示.
△ABC在方格中的位置如图所示.分析 (1)利用点A和点B的坐标建立直角坐标系,然后写出C点坐标;
(2)利用关于x轴对称的点的坐标特征写出点A、B、C的对应点A1、B1、C1的坐标,在描点即可得到△A1B1C1;利用利用原点对称的点的坐标特征,写出点A、B、C的对应点A2、B2、C2的坐标,然后描点即可得到△A2B2C2.
解答 解:(1) 如图,C点坐标为(3,-3);
如图,C点坐标为(3,-3);
(2)如图,△A1B1C1、△A2B2C2为所作,C1、C2两点的坐标分别为(3,3)、(-3,3).
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


科目:初中数学 来源: 题型:解答题
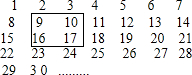 把连续的正整数1,2,3,4,…,按如图方式列成一个数表.
把连续的正整数1,2,3,4,…,按如图方式列成一个数表.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
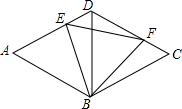 如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.
如图,已知菱形ABCD的边长为4,对角线BD=4,点E,F分别在菱形的边AD,CD上滑动(点E,F均不与点A,C,D重合),且满足AE+CF=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
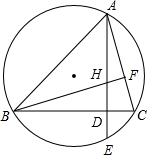 如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.
如图,已知:△ABC的顶点在⊙O上,高AD、BF相交于点H,AD的延长线于⊙O交于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com