
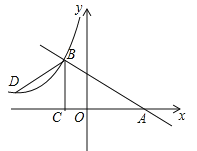
【题目】如图,已知一次函数y=kx+b的图象与x轴交于点A,与反比例函数![]() (x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(x<0)的图象交于点B(﹣2,n),过点B作BC⊥x轴于点C,点D(3﹣3n,1)是该反比例函数图象上一点.
(1)求m的值;
(2)若∠DBC=∠ABC,求一次函数y=kx+b的表达式.
【答案】(1)-6;(2)![]() .
.
【解析】试题分析:(1)由点B(﹣2,n)、D(3﹣3n,1)在反比例函数![]() (x<0)的图象上可得﹣2n=3﹣3n,即可得出答案;
(x<0)的图象上可得﹣2n=3﹣3n,即可得出答案;
(2)由(1)得出B、D的坐标,作DE⊥BC.延长DE交AB于点F,证△DBE≌△FBE得DE=FE=4,即可知点F(2,1),再利用待定系数法求解可得.
试题解析:(1)∵点B(﹣2,n)、D(3﹣3n,1)在反比例函数![]() (x<0)的图象上,∴
(x<0)的图象上,∴![]() ,解得:
,解得:![]() ;
;
(2)由(1)知反比例函数解析式为![]() ,∵n=3,∴点B(﹣2,3)、D(﹣6,1),
,∵n=3,∴点B(﹣2,3)、D(﹣6,1),
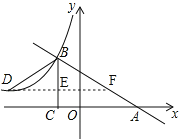
如图,过点D作DE⊥BC于点E,延长DE交AB于点F,
在△DBE和△FBE中,∵∠DBE=∠FBE,BE=BE,∠BED=∠BEF=90°,
∴△DBE≌△FBE(ASA),∴DE=FE=4,
∴点F(2,1),将点B(﹣2,3)、F(2,1)代入y=kx+b,
∴![]() ,解得:
,解得: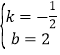 ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
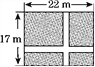
【题目】如图,在一块长为22 m,宽为17 m的矩形地面上,要修建同样宽的两条互相垂直的道路(两条道路各与矩形的一条边平行),剩余部分种上草坪,使草坪面积为300 m2.若设道路宽为x m,根据题意可列出方程为______________________________.
【答案】(22-x)(17-x)=300(或x2-39x+74=0)
【解析】试题分析:把所修的两条道路分别平移到矩形的最上边和最左边,则剩下的草坪是一个长方形,根据长方形的面积公式列方程.设道路的宽应为x米,由题意有(22﹣x)(17﹣x)=300,故答案为:(22﹣x)(17﹣x)=300.
考点:由实际问题抽象出一元二次方程.
【题型】填空题
【结束】
17
【题目】x=1是关于x的一元二次方程x2+mx﹣5=0的一个根,则此方程的另一个根是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③DP2=PHPC;④FE:BC=![]() ,其中正确的个数为( )
,其中正确的个数为( )
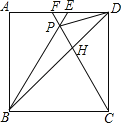
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,对称轴为直线x = -2的抛物线经过点C(0,2),与x轴交于A(-3,0)、B两点(点A在点B的左侧).
(1)求这条抛物线的表达式.
(2)连接BC,求∠BCO的余切值.
(3)如果过点C的直线,交x轴于点E,交抛物线于点P,且∠CEO =∠BCO,求点P的坐标.
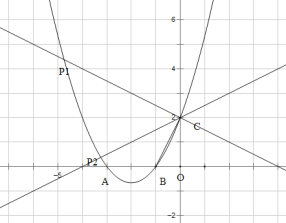
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的图象的一部分,给出下列命题:
①a+b+c=0;
②b>2a;
③ax2+bx+c=0的两根分别为﹣3和1;
④c=﹣3a,
其中正确的命题是( )
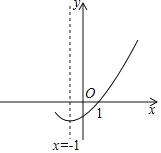
A.①②B.②③C.①③D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
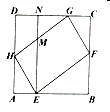
【题目】如图,平行四边形![]() 的四个顶点分别在正方形
的四个顶点分别在正方形![]() 的四条边上.
的四条边上.![]() ,分别交
,分别交![]() ,
,![]() ,
,![]() 于点
于点![]() ,
,![]() ,
,![]() ,且
,且![]() .要求得平行四边形
.要求得平行四边形![]() 的面积,只需知道一条线段的长度.这条线段可以是( )
的面积,只需知道一条线段的长度.这条线段可以是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果公司新购进10000千克柑橘,每千克柑橘的成本为9元. 柑橘在运输、存储过程中会有损坏,销售人员从所有的柑橘中随机抽取若干柑橘,进行“柑橘损坏率”统计,并把获得的数据记录如下:
柑橘总重量n/千克 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 450 | 500 |
损坏柑橘重量m/千克 | 5.50 | 10.50 | 15.15 | 19.42 | 24.25 | 30.93 | 35.32 | 39.24 | 44.57 | 51.54 |
柑橘损坏的频率 | 0.110 | 0.105 | 0.101 | 0.097 | 0.097 | 0.103 | 0.101 | 0.098 | 0.099 | 0.103 |
根据以上数据,估计柑橘损坏的概率为 (结果保留小数点后一位);由此可知,去掉损坏的柑橘后,水果公司为了不亏本,完好柑橘每千克的售价至少为________元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
学习函数知识后,对于一些特殊的不等式,我们可以借助函数图象来求出它的解集,例如求不等式x﹣3>![]() 的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=
的解集,我们可以在同一坐标系中,画出直线y1=x﹣3与函数y2=![]() 的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>
的图象(如图1),观察图象可知:它们交于点A(﹣1,﹣4),B(4,1).当﹣1<x<0,或x>4时,y1>y2,即不等式x﹣3>![]() 的解集为﹣1<x<0,或x>4.
的解集为﹣1<x<0,或x>4.
小东根据学习以上知识的经验,对求不等式x3+3x2﹣x﹣3>0的解集进行了探究.下面是小东的探究过程,请补充完整:
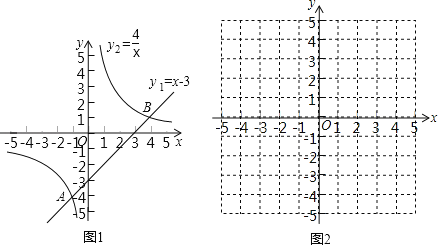
(1)将不等式按条件进行转化:当x=0时,原不等式不成立;x>0时,原不等式转化为x2+3x﹣1>![]() ;当x<0时,原不等式转化为______;
;当x<0时,原不等式转化为______;
(2)构造函数,画出图象:设y3=x2+3x﹣1,y4=![]() ,在同一坐标系(图2)中分别画出这两个函数的图象.
,在同一坐标系(图2)中分别画出这两个函数的图象.
(3)借助图象,写出解集:观察所画两个函数的图象,确定两个函数图象交点的横坐标,结合(1)的讨论结果,可知:不等式x3+3x2﹣x﹣3>0的解集为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com