Question

4．已知，点A （10，0）、B（6，8），点P为线段OA上一动点（不与点A、点O重合），以PA为半径的⊙P与线段AB的另一个交点为C，作CD⊥OB于D（如图①）．
（1）判断△OAB是否是等腰三角形，并求sin∠BOA的值；
（2）求证：CD是⊙P的切线；
（3）求当⊙P与OB相切时⊙P的半径；
（4）在（3）的情况下，设（3）中⊙P与OB的切点为E，连结PB交CD于点F（如图②）①求CF的长；②在线段DE上是否存在点G使∠GPF=45°？若存在，求出EG的长；若不存在，请说明理由．

Answer 1

分析 （1）过点B作BN⊥x轴于N，由勾股定理可得OB，易得△OAB是等腰三角形，由锐角三角函数定义可得sin∠BOA的值；
（2）连结PC，利用等腰三角形的性质证得PC∥OB，由平行线的性质可得结论；
（3）如图1．设⊙P的半径为r，在Rt△OPE中，由（1）中结论可知sin∠EOP=$\frac{PE}{OP}$=$\frac{r}{10-r}$=$\frac{4}{5}$，解得r；
（4）①如图2．证得△BDF∽△PCF，由（2）知r=$\frac{40}{9}$，利用相似三角形的性质可得CF；
②在线段DE上存在点G使∠GPF=45°，（如图3）在DE延长线上截取ET=FC，易得△PET≌△PCF，△PGT≌△PGF，由全等三角形的性质可得GF=TG=TE+EG=CF+EG，设GE=a，则GD=$\frac{40}{9}-a$，GF=CF+EG=$\frac{80}{27}+a$，由勾股定理可得EG的长．

解答 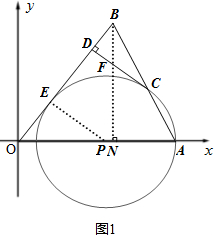解：（1）过点B作BN⊥x轴于N，
∵BN=8，ON=6，
在Rt△OBN中，OB=$\sqrt{{ON}^{2}{+BN}^{2}}$=$\sqrt{{6}^{2}{+8}^{2}}$=10，
∴OB=OA=10，故△OAB是等腰三角形，
sin∠BOA=$\frac{BN}{OB}$=$\frac{8}{10}$=$\frac{4}{5}$；

（2）连结PC，
∵PC=PA，
∴∠1=∠2，
又∵OA=OB，
∴∠OBA=∠1，
∴∠OBA=∠2，
∴PC∥OB，
∵CD⊥OB，
∴CD⊥PC，
∴CD是⊙P的切线；

（3）如图1．设⊙P的半径为r，
∵⊙P与OB相切于点E，
∴OB⊥PE，
∴在Rt△OPE中，sin∠EOP=$\frac{PE}{OP}$=$\frac{r}{10-r}$=$\frac{4}{5}$，
解得：r=$\frac{40}{9}$；

（4）①如图2．
∵由（2）知r=$\frac{40}{9}$，
∴在Rt△OPE中，
OE=$\sqrt{{OP}^{2}{-PE}^{2}}$=$\sqrt{{（10-\frac{40}{9}）}^{2}{-（\frac{40}{9}）}^{2}}$=$\frac{10}{3}$，
∵∠PCD=∠CDE=∠PED=90°，
∴四边形PCDE为矩形．
∵PE=PC，
∴矩形PCDE为正方形．
∴DE=DC=r=$\frac{40}{9}$，
∴BD=OB-OE-DE=10-$\frac{10}{3}-\frac{40}{9}$=$\frac{20}{9}$，
∵∠BFD=∠PFC，∠PEO=∠PCF=90°，
∴△BDF∽△PCF，
∴$\frac{DF}{CF}=\frac{BD}{PC}$，
 即$\frac{\frac{40}{9}-CF}{CF}=\frac{\frac{20}{9}}{\frac{40}{9}}$
解得：CF=$\frac{80}{27}$，DF=$\frac{40}{27}$；
②解法一：在线段DE上存在点G使∠GPF=45°（如图3），
在DE延长线上截取ET=FC，
∵四边形PCDE为正方形，
∴∠PCF=∠PEO=90°，PC=EC，
∴△PET≌△PCF，
∴∠3=∠4，PF=PT，
∵∠CPE=90°，∠GPF=45°，
∴∠3+∠GPE=∠CPE-∠GPF=45°，
∴∠TPG=∠4+∠GPE=∠3+∠GPE=45°，
∴∠GPF=∠TPG，
∵PF=PT，∠GPF=∠TPG，PG=PG，
∴△PGT≌△PGF，
∴GF=TG=TE+EG=CF+EG
设GE=a，则GD=$\frac{40}{9}-a$，GF=CF+EG=$\frac{80}{27}+a$，
∵在Rt△DFG中，DF²+DG²=GF²，
∴${（\frac{40}{27}）}^{2}$${+（\frac{40}{9}-a）}^{2}$=${（\frac{80}{27}+a）}^{2}$，
解得：a=$\frac{8}{9}$，
∴$GE=\frac{8}{9}$；
解二：在线段DE上存在点G使∠GPF=45°（如图4），
在EP上截取EQ=EG，
∵OB⊥PE，
∴∠GQE=45°，
∴∠GQP=135°，
∵四边形PCDE为正方形，
∴PD=$\sqrt{2}PC$=$\frac{40}{9}$$\sqrt{2}$，∠EPD=∠PDC=45°，
∴∠4+∠5=45°，
∵∠FPG=45°，
∴∠3+∠5=45°，
∴∠3=∠4，
∵∠BDP=∠BDC+∠PDC=90°+45°=135°，
∴∠GQP=∠BDP，
∴△GQP∽△BDP，
∴$\frac{GQ}{BD}=\frac{PQ}{PD}$，
∵OE=$\frac{10}{3}$，DE=$\frac{40}{9}$，OB=10，
∴BD=OB-ED-OE=$\frac{20}{9}$，
设EG=a，则GQ=$\sqrt{2}$a，PQ=PE-EQ=$\frac{40}{9}-a$，
∴$\frac{\sqrt{2}a}{\frac{20}{9}}=\frac{\frac{40}{9}-a}{\frac{40}{9}\sqrt{2}}$，
解得：a=$\frac{8}{9}$，
∴EG=$\frac{8}{9}$．

点评 本题主要考查了切线的性质及判定定理，矩形的性质，全等三角形的性质及判定，勾股定理等，作出适当的辅助线，综合运用各定理是解答此题的关键．