
【题目】如图,在△ABC中,AB =AC=2,∠B = 40°,点D在线段BC上运动(不与点B,C重合),连接AD,作∠ADE = 40°,DE交线段AC于点E.
(1)当∠BDA = 115°时,∠BAD= °,∠DEC = °,当点D从点B向点C运动时,∠BDA逐渐变 (填“大”或“小”) .
(2)当DC等于多少时,△ABD≌△DCE?请说明理由.
(3)在点D的运动过程中,是否存在△ADE是等腰三角形?若存在,请直接写出此时∠BDA的度数;若不存在,请说明理由.

【答案】(1)25,115,小;(2)当DC=2时,△ABD ≌△DCE,理由见解析;(3)存在.∠BDA=110°或80°.
【解析】试题分析:
(1)根据三角形的内角和计算∠BAD,再由三角形的一个外等于和它不相邻的两个内角的和求∠EDC,从而可得∠DEC,根据三角形的内角和判断∠BDA的大小变化.
(2)在(1)中可得到这两个三角形的三个角都相等,只要有一条边对应相等即可,而已知AB=2,所以CD=2.
(3)假设等腰△ADE存在,因为底边不确定,所以需要分三种情况讨论,求出∠BDA的度数后要检验.
试题解析:
(1)∠BAD=180°-∠B-∠BDA=180°-40°-115°=25°.
∵∠ADC=∠B+∠BAD,∴40°+∠EDC=40°+∠BAD,∴∠EDC=∠BAD.
∴∠DEC=180°-∠C-∠EDC=180°-40°-25°=115°.
∵在点D从点B向点C运动的过程中,对于△ABD,∠B=40°不变,∠BAD逐渐变大,
∴∠ADB逐渐变小.
(2)当DC=2时,△ABD≌△DCE,理由如下:
在△ABD和△DCE中,
因为∠B=∠C,∠BAD=∠CDE,已经有了两个角分别相等,所以只需要一边对应相等即可.
AB=AC=2,当DC=AB时,则可用ASA证明这两个三角形全等.
(3)在点D的运动过程中,存在△ADE是等腰三角形。理由如下:
①当DA=DE时,∠DAE=(180°-∠ADE)÷2=(180°-40°)÷2=70°.
所以∠BDA=∠C+∠DAE=40°+70°=110°.
②当AD=AE时,∠DAE=180°-2×40°=100°,
所以∠BDA=∠C+∠DAE=40°+100°=140°,
但∠BDA=180°-∠B-∠BAD=180°-40°-∠BAD,所以∠BDA<140°,
所以AD=AE不存在.
③当EA=ED时,∠DAE=∠EDA=40°,
所以∠BDA=∠DAE+∠C=40°+40°=80°.
综上所述,∠BDA=110°或80°.


科目:初中数学 来源: 题型:
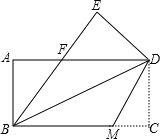
【题目】如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠BAD=∠ACB=90°,AB=AD,AC=4BC,设CD的长为x,四边形ABCD的面积为y,则y与x之间的函数关系式是( )
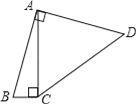
A. y=![]() B. y=
B. y=![]() C. y=
C. y=![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某完全中学(含初、高中)篮球队12名队员的年龄情况如下:
年龄(单位:岁) | 14 | 15 | 16 | 17 | 18 |
人 数 | 1 | 4 | 3 | 2 | 2 |
(1)这个队队员年龄的众数是 ,中位数是 ;
(2)求这个队队员的平均年龄;
(3)若把这个队队员年龄绘成扇形统计图,请求出年龄为15岁对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
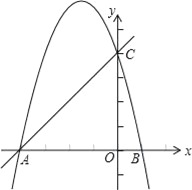
【题目】如图,抛物线y=ax2﹣bx﹣4a交x轴于点A、B,交y轴于点C,其中点B、C的坐标分别为B(1,0)、C(0,4).
(1)求抛物线的解析式,并用配方法把其化为y=a(x﹣h)2+k的形式,写出顶点坐标;
(2)已知点D(m,1﹣m)在第二象限的抛物线上,求出m的值,并直接写出点D关于直线AC的对称点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,AB∥DE,AC∥DF,AC=DF下列条件中,不能判断△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,半径为1的⊙A圆心与原点O重合,直线l分别交x轴、y轴于点B、C,若点B的坐标为(6,0),tan∠ABC=![]() .
.

(1)若点P是⊙A 上的动点,求P到直线BC的最小距离,并求此时点P的坐标;
(2)若点A从原点O出发,以1个单位/秒的速度沿着线路OB→BC→CO运动,回到点O停止运动,⊙A随着点A的运动而移动.设点A运动的时间为t.
①求⊙A在整个运动过程中与坐标轴相切时t的取值;
②求⊙A在整个运动过程中所扫过的图形的面积为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com